Question

Two slits are separated by 0.320 mm. A beam of 500 nm light strikes the slits, producing an interference pattern. Determine the number of maxima observed in the angular range \[-{{30}^{0}}<\theta <+{{30}^{0}}\].

Answer 1

Hint: We need to understand the relation between the wavelength of the light used to create the interference pattern, its slit width and the angular range from the slit with the number of maxima that can be observed using the particular situation here.

Complete Step-by-Step Solution:
We are given an interference arrangement in which the slit width is 0.032 mm. A light of wavelength 500 nm is used in order to obtain the interference pattern. We know that the number of maxima or number minima formed due to a slit and a particular wavelength will be constant within a given range.

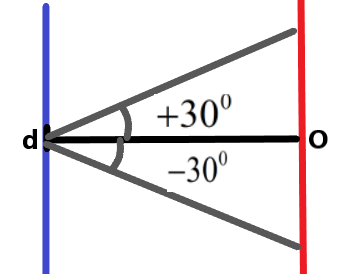
The relation between the slit width of the slit used in the setup and the wavelength of the light used will be related to each other as –
\[d\sin \theta =n\lambda \]
Where d is the slit width, n is the number of maxima or minima from the central fringe to one end, \[\theta \] is the angle between the central point and the maximum distance from the center and \[\lambda \] is the wavelength of the light used.

We can find the number of maxima or minima as –
\[\begin{align}
  & d\sin \theta =n\lambda \\
 & \Rightarrow n=\dfrac{d\sin \theta }{\lambda } \\
 & \Rightarrow n=\dfrac{0.32\times {{10}^{-3}}m\times \sin \theta }{500\times {{10}^{-9}}m} \\
 & \Rightarrow n=\dfrac{0.32\sin {{30}^{0}}}{5\times {{10}^{-4}}} \\
 & \Rightarrow n=\dfrac{0.32\times \dfrac{1}{2}}{5\times {{10}^{-4}}} \\
 & \therefore n=320 \\
\end{align}\]

The number of maxima on one side will be 360. So, the total number of maxima including the central maxima will be –
\[\begin{align}
  & {{n}_{total}}=n+n+1 \\
 & \Rightarrow {{n}_{total}}=320+320+1 \\
 & \therefore {{n}_{total}}=641 \\
\end{align}\]

The total number of maxima in the angular range of \[-{{30}^{0}}<\theta <+{{30}^{0}}\] is 641. This is the required solution.

Note:
The number of maxima in the interference pattern and the number of minima in the same pattern will be the same. The only difference is the central pattern which doesn’t have the minima as the principal maxima covers the minima in this central region.