Question

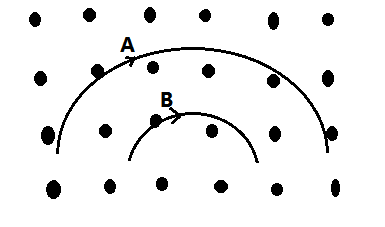
Two particles $A$ and $B$ of masses ${m_A}$ and ${m_B}$ respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speed of the particles is ${v_A}$ and ${v_B}$​ respectively, and the trajectories are as shown in the figure. Then

A. ${m_A}{v_A} < {m_B}{v_B}$
B. ${m_A}{v_A} > {m_B}{v_B}$
C. ${m_A} < {m_B}$ and ${v_A} < {v_B}$
D. ${m_A} = {m_B}$ and ${v_A} = {v_B}$

Answer 1

Hint: Here we see that the uniform magnetic field is perpendicular to the plane in which the two particles $A$ and $B$ of masses ${m_A}$ and ${m_B}$respectively and having the same charge are moving. When any charge particle moves perpendicular to the existing uniform magnetic field then the force which will act due to the interaction of magnetic field and charge particle will act as centripetal force and thus the particle will perform the circular motion.

Complete step by step answer:
As we know that the path of a charge particle in a uniform magnetic field is circular so the formula for the radius of the circle will be,
$r = \dfrac{{mv}}{{qB}}$, where $m = $mass of the charge particle, $v = $velocity of the charge particle, $q = $charge on the particle, $B = $external magnetic field.
Here we see that the external magnetic field and charge on the particle is the same for both the particles.
So, the mass and the velocity of the charge particles will determine the radius of the circle which is made by the motion of the particles.
From the diagram we see that the ${r_A} > {r_B}$
And mass and velocities both are directly proportional to the radius.
So, the mass of particle $A$ is more than that of the $B$.
i.e. ${m_A} > {m_B}$-----equation (2)
and the velocities will also be having the same relation as that of the mass, that means the velocity of $A$ will be more than that of the $B$.
i.e. ${v_A} > {v_B}$----equation (2)
so, on combining both the equations (equation (1) and equation (2)), we get
i.e. ${m_A}{v_A} > {m_B}{v_B}$
Hence the option (B) is the correct answer.

Note:
If we consider a general situation in which the charge particle is moving with some velocity in an external magnetic field then the force that will be acting on the particle will not perform any work on the charge particle. Therefore, the energy of a charged particle cannot be increased by the use of the magnetic field. Here in this given condition velocity and magnetic field are perpendicular to each other which makes the particle to perform the circular motion and this property is used in accelerator and fusion applications.