Question

Two inductances $ {L_1} $ ​ and $ {L_2} $ ​ are connected in series and are separated by a large distance:
(i) Show that their equivalent inductance is $ {L_1} + {L_2} $ ​.
(ii) Why must their separation be large?

Answer 1

Hint : Using the current-inductance and the voltage-inductance relation, which is given by the formula $ V = L\dfrac{{di}}{{dt}} $ . Using this equation and Kirchhoff’s voltage law, solve for the overall inductance value.

Complete step by step answer
To show that the equivalent inductance is the sum of the inductances present in the circuit, let us consider a circuit, that has a source V and current I flowing through it , consisting of two inductors $ {L_1} $ and $ {L_2} $ that are connected in series .
The diagram of the same is given below,

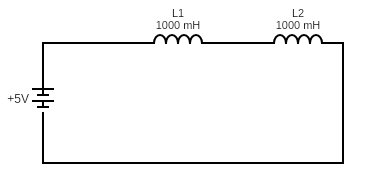
Now, applying Kirchhoff’s voltage law in the circuit,
 $ V = V{L_1} + V{L_2} $ (Since V is constant throughout the circuit)
Now, according to our solution hint, Voltage of an inductor circuit is given as the product of Overall inductance of the circuit and the rate of change of current in the circuit with respect to time period.
 $ V = L\dfrac{{di}}{{dt}} $
Substituting the V value in the above mentioned Kirchhoff’s law equation
 $ L\dfrac{{di}}{{dt}} = {L_2}\dfrac{{di}}{{dt}} + {L_1}\dfrac{{di}}{{dt}} $
Cancelling out the common differentiated term we get,
 $ \Rightarrow L = {L_2} + {L_1} $
Hence, It is evident that the total inductance of the circuit is the sum of the individual inductance of the inductors.
ii) Now , we have found how total resistance is calculated , we need to state why the distance between one inductor and the other must be large. When inductors are connected in series, the magnetic field of one inductor links with the other and their effect of mutual inductance. Mutually connected inductors are said to oppose the total inductance value which can cause the value to increase or decrease due to leakage. Now this inductance leakage can cause severe adverse effects in the circuit. Hence it is necessary that the coils are kept apart.

Note
Kirchhoff’s Voltage law states that for a closed series loop the total voltage flowing in the loop is equal to the algebraic sum of all voltage drops within the circuit loop.