Question

Two capacitors $C_1$ and $C_2$ are charged to 120V and 200V respectively. It is found that by connecting them together the potential on each one can be made zero. Then,
A) $3\mathop C\nolimits_1 = 5\mathop C\nolimits_2 $
B) $3\mathop C\nolimits_1 + 5\mathop C\nolimits_2 $
C) $9\mathop C\nolimits_1 = 4\mathop C\nolimits_2 $
D) $5\mathop C\nolimits_1 = 3\mathop C\nolimits_2 $

Answer 1

Hint: In this question, use the relationship between the capacitance, charge and potential of a capacitor that is $Q = CV$. Use the constraints given in the question to find the charge onto the two capacitors. Then use the fact that since the potential is found to be zero therefore the capacitors must be connected in phase opposition that is \[\mathop Q\nolimits_1 - \mathop Q\nolimits_2 = 0\]. This will help to get the right answer to this problem.

Complete answer:

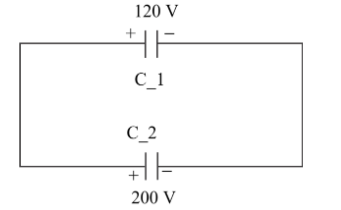
As we know the charge stored by the capacitor is the product of individual capacitance and the voltage stored in the capacitor.
$ \Rightarrow Q = CV$……. (1)
Where Q= charge, C= capacitance, V= voltage
Now, let the capacitance of the first capacitor be $\mathop C\nolimits_1 $and the capacitance of the second capacitor be $\mathop C\nolimits_2 $
The charged voltage of the first and second capacitor are 120V and 200V.
So, the charges on the first and capacitors are
$\mathop Q\nolimits_1 = 120\mathop C\nolimits_1 $coulomb
AND
$\mathop Q\nolimits_2 = 200\mathop C\nolimits_2 $coulomb
Now it is given that they are connected in parallel and it is found that the potential on each of them is zero so from equation (1) if the potential or voltage on each of them is zero then the charge on each of them is zero.
It is only possible when they are connected in phase opposition such that \[\mathop Q\nolimits_1 - \mathop Q\nolimits_2 = 0\]
Now, substitute the value in above equation we have,
\[\mathop Q\nolimits_1 - \mathop Q\nolimits_2 = 0\]
$ \Rightarrow 120\mathop C\nolimits_1 - 200\mathop C\nolimits_2 = 0$
Now, simplify this we have
$ \Rightarrow 120\mathop C\nolimits_1 = 200\mathop C\nolimits_2 $
Divide by 40 throughout we have,
$3\mathop C\nolimits_1 = 5\mathop C\nolimits_2 $

$\therefore$ The required relation between $\mathop C\nolimits_1 $ and $\mathop C\nolimits_2 $ i.e first and second capacitor. Hence, option (A) is the correct answer.

Note:
The parallel combinatory of the capacitors is exactly equivalent to that series connection of the resistors$\mathop C\nolimits_{eq} = \mathop C\nolimits_1 + \mathop C\nolimits_2 $. It is advised to remember the direct relationship that is q=cv. A parallel plate capacitor is formed by charging parallel plates which may have dielectric or air-filled in between the plates. these plates are separated by some distance d and if A is the area of cross-section of the plates then capacitance $C$ is given by $C=\dfrac{{\epsilon}_o A}{d}$