Question

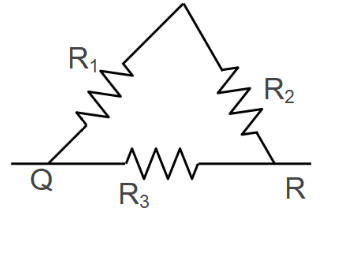
Tree resistors each of $2$ ohm is connected together in a triangular shape. The resistance between any two vertices will be?

a) $\dfrac{4}{3} ohm$
b) $\dfrac{3}{4} ohm$
c) $3 ohm$
d) $6 ohm$

Answer 1

Hint: First observe the diagram carefully, those resistors which are connected end to end, they are in series. The equivalent resistance of resistors connected in series will be the sum of resistances. Those resistors having negative and positive terminals are in common, they are in parallel.

Complete step-by-step solution:
Three resistors each of $2$ ohm is connected together in a triangular shape.
$R_{1} = 2 ohm$
$R_{2} = 2 ohm$
$R_{3} = 2 ohm$

We will simplify this circuit.

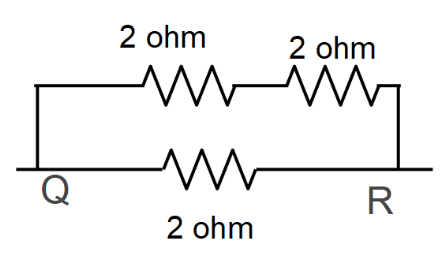
$R_{1}$ and $R_{2}$ are connected in series. So, the equivalent resistance of both resistor is:
$2+2 = 4 ohm$

Now $4 ohm$ and $2 ohm$ are connected in parallel to each other. Now we will find the equivalent resistance of both the resistors:
$R_{QR} = \dfrac{4 \times 2}{4+2}$
$R_{QR} = \dfrac{8}{6} ohm$
$R_{QR} = \dfrac{4}{3} ohm$
The resistance between any two vertices will be $\dfrac{4}{3} ohm$.

Note: If two different conductors are put in a circuit, then the current amount to move in each may not be equal. There are several reasons:
First: The ease with which electrons can move within the composition of the material. If the electrons are tied tightly to the crystal structure, it will not be obvious to pull them free to be adrift of electrons in a unique direction. In other materials, many free electrons are drifting randomly around the structure. It is these materials that enable a current to move more quickly.
Second: Length of electrical resistance of a material. The more petite the length of the material, the smaller its overall resistance.
Third: the cross-sectional area. The extended the cross-sectional area, the lesser the resistance will be as there is a broader area through which the current can pass.