Question

To decrease the range of an ammeter, its resistance needs to be increased. An ammeter has resistance $R_0$ and range I. Which of the following resistance can be connected in series with it to decrease its range to I/n?

A. $\dfrac{R_0}{n}$
B. $\dfrac{R_0}{(n-1)}$
C. $\dfrac{R_0}{(n+1)}$
D. None of these.

Answer 1

Hint: We need to find the resultant current when a resistor is connected in series. In a series circuit, the current is common. By applying the ohm’s law to the series circuit, we find the resistance.

Formula used:
Ohm’s law: When a potential difference of V volts is applied to a resistance R and I current flows through it the relationship of V and I can be written as:
V=IR

Complete answer:
 An ammeter is a device which measures the amount of current in the circuit when it is connected in series. In an analog ammeter, we have a scale that goes from a minimum (usually 0 units) to a maximum value (says I in the question). Thus, the maximum value that our ammeter depicts is I (units) when it has a resistance of $R _0$. Consider this circuit as equivalent to a situation when I am flowing through a resistance of $R _0$ when a battery of V volts is connected.

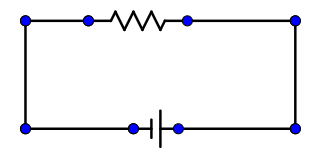
V=I$R _0$

We need to find a resistance to be attached in series with this resistance $R _0$ so that the current reduces to I/n in the circuit (we still use our V volts supply). So now, the battery of ours has to give current to two resistances R and R’:

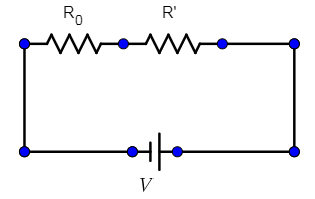
V=$\dfrac{I}{n}$ ($R _0$ +R’)

Thus, we must equate the V in both circuits to get our value of R’:
IR₀=$\dfrac{I}{n}$ ($R _0$ +R’)
$R _0$ -$\dfrac{1}{n}$ $R _0$ =$\dfrac{R’}{n}$

This gives,
(n-1) $R _0$ =R’
So, the correct answer is “Option D”.

Note:
An ammeter is connected in series in a circuit so the resistance it has is accounted for in series in the circuit whereas if there were a voltmeter, it would have had a resistance in parallel with the circuit, across some other resistance.