Questions & Answers
Question
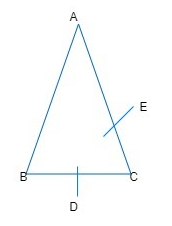
AnswersThree charges each have $ +q $ charge, are placed at the corner of an isosceles triangle ABC of sides BC and AC, 2a.D and E are the mid points of BC and CA. The work done in taking a charge Q from D to E is:
(A) $ \dfrac{eqQ}{8\pi {{\in }_{0}}a} $
(B) $ \dfrac{qQ}{4\pi {{\in }_{0}}a} $
(C) Zero
(D) $ \dfrac{3qQ}{4\pi {{\in }_{0}}a} $
Answer
Verified91.5k+ views
Hint: To find out the work done is taking charge Q from one point to another, we will find electrostatic potential at those points using
$ V=\dfrac{q}{4\pi {{\in }_{0}}r} $
$ V $ is the potential generated between the charges
$ q $ is the charge due to which our test charge is affected
r is the distance between the charges.
Complete step by step solution
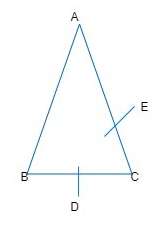
Here,
$ AC=BC=2a $
As D and E are midpoints of BC and AC (given).
$ \therefore $ $ AE=EC=a $
And,
$ BD=DC=a $
In $ \Delta ADC, $
$ \begin{align}
& {{(AD)}^{2}}={{(AC)}^{2}}-{{(DC)}^{2}} \\
& ={{(2a)}^{2}}-{{(a)}^{2}}={{(4a)}^{2}}-{{(a)}^{2}}={{(a)}^{2}} \\
& AD=a\sqrt{3} \\
\end{align} $
Similarly, potential at points D due to the given charge distribution is
$ {{V}_{D}}=\dfrac{1}{4\pi {{\in }_{0}}}[\dfrac{q}{BD}+\dfrac{q}{DC}+\dfrac{q}{AD}] $
$ \begin{align}
& =\dfrac{q}{4\pi {{\in }_{0}}}\left[ \dfrac{1}{a}+\dfrac{1}{a}+\dfrac{1}{\sqrt{3}a} \right] \\
& =\dfrac{q}{4\pi {{\in }_{0}}a}\left[ 2+\dfrac{1}{\sqrt{3}} \right] \\
\end{align} $ ...........................(1)
Potential at point E due to given charge configuration is
$ {{V}_{E}}=\dfrac{1}{4\pi {{\in }_{0}}}\left[ \dfrac{1}{q}+\dfrac{1}{q}+\dfrac{1}{a\sqrt{3}} \right] $
$ =\dfrac{q}{4\pi {{\in }_{0}}a}\left[ 2+\dfrac{1}{\sqrt{3}} \right] $ ...........................(2)
From (1) and (2), it is clear that
The work done in taking a charge Q from D to E is
$ W=Q({{V}_{E}}-{{V}_{D}})=0 $ $ (\because {{V}_{D}}={{V}_{E}}) $
Therefore, option (C) is correct.
Note
Electric potential due to single charge is spherically symmetric. It should be clearly borne in mind that due to single charge,
$ F\propto \dfrac{1}{{{r}^{2}}} $ ; $ E\propto \dfrac{1}{{{r}^{2}}} $ but $ V\propto \dfrac{1}{r} $ ,
where r is the distance from the charge.
$ V=\dfrac{q}{4\pi {{\in }_{0}}r} $
$ V $ is the potential generated between the charges
$ q $ is the charge due to which our test charge is affected
r is the distance between the charges.
Complete step by step solution
Here,
$ AC=BC=2a $
As D and E are midpoints of BC and AC (given).
$ \therefore $ $ AE=EC=a $
And,
$ BD=DC=a $
In $ \Delta ADC, $
$ \begin{align}
& {{(AD)}^{2}}={{(AC)}^{2}}-{{(DC)}^{2}} \\
& ={{(2a)}^{2}}-{{(a)}^{2}}={{(4a)}^{2}}-{{(a)}^{2}}={{(a)}^{2}} \\
& AD=a\sqrt{3} \\
\end{align} $
Similarly, potential at points D due to the given charge distribution is
$ {{V}_{D}}=\dfrac{1}{4\pi {{\in }_{0}}}[\dfrac{q}{BD}+\dfrac{q}{DC}+\dfrac{q}{AD}] $
$ \begin{align}
& =\dfrac{q}{4\pi {{\in }_{0}}}\left[ \dfrac{1}{a}+\dfrac{1}{a}+\dfrac{1}{\sqrt{3}a} \right] \\
& =\dfrac{q}{4\pi {{\in }_{0}}a}\left[ 2+\dfrac{1}{\sqrt{3}} \right] \\
\end{align} $ ...........................(1)
Potential at point E due to given charge configuration is
$ {{V}_{E}}=\dfrac{1}{4\pi {{\in }_{0}}}\left[ \dfrac{1}{q}+\dfrac{1}{q}+\dfrac{1}{a\sqrt{3}} \right] $
$ =\dfrac{q}{4\pi {{\in }_{0}}a}\left[ 2+\dfrac{1}{\sqrt{3}} \right] $ ...........................(2)
From (1) and (2), it is clear that
The work done in taking a charge Q from D to E is
$ W=Q({{V}_{E}}-{{V}_{D}})=0 $ $ (\because {{V}_{D}}={{V}_{E}}) $
Therefore, option (C) is correct.
Note
Electric potential due to single charge is spherically symmetric. It should be clearly borne in mind that due to single charge,
$ F\propto \dfrac{1}{{{r}^{2}}} $ ; $ E\propto \dfrac{1}{{{r}^{2}}} $ but $ V\propto \dfrac{1}{r} $ ,
where r is the distance from the charge.
Students Also Read