
There is no ring strain in cyclohexane, but cyclobutane has an angle strain of ${{9}^{{}^\circ }}{{44}^{'}}$. If $\Delta H_{c}^{\circ }$of cyclohexane per $\left( C{{H}_{2}} \right)$ group is 660 KJ/mol and $\Delta H_{c}^{\circ }$ of cyclobutane is 2744 KJ/mol, what is the ring strain in KJ/mol for cyclobutane?
[A] -104
[B] 104
[C] -2084
[D] 2084
Answer
588.3k+ views
Hint: To solve this question, we can use the $\Delta H_{c}^{\circ }$ value of each $\left( C{{H}_{2}} \right)$ groups and the cyclobutane. We can find out the ring strain by subtracting the $\Delta H_{c}^{\circ }$ value of each $\left( C{{H}_{2}} \right)$group present in cyclobutane by the $\Delta H_{c}^{\circ }$ value of cyclobutane. The total number of $\left( C{{H}_{2}} \right)$ groups in cyclobutane is four.
Complete answer:
We know that ring strain in organic molecules is a form of instability that exists when the angles formed between the molecules are unstable.
We observe ring strain generally in smaller organic molecules like cyclobutane and cyclopropane.
In the given question, we have that the cyclobutane has an angle strain of ${{9}^{{}^\circ }}{{44}^{'}}$. We know that there are four $C{{H}_{2}}$ groups in cyclobutane and we can draw its structure as-
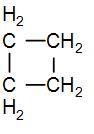
As we can see from the above diagram that there are 4 $C{{H}_{2}}$ groups. So to find the ring strain in cyclobutane, we can subtract the standard enthalpy of combustion of each of these $C{{H}_{2}}$ groups from the standard enthalpy of combustion of cyclobutane.
Therefore, we can write that-
Ring strain = $4\times \Delta H_{c}^{\circ }$ of each $C{{H}_{2}}$ group.-$\Delta H_{c}^{\circ }$of cyclobutane
Therefore, ring strain = $\left( 4\times 660 \right)$KJ/mol - 2274 KJ/mol =140 KJ/mol.
From the above calculation it is clear that ring strain in a cyclobutane ring is 104 KL/mol.
So, the correct answer is “Option B”.
Note: Ring strain is mostly caused due to the $s{{p}^{3}}$ hybridised carbons which are present in the cycloalkanes. For a ring to not be strained the ideal angle is ${{109.5}^{{}^\circ }}$ but due to the $s{{p}^{3}}$ hybridised carbons, the bond angle is not maintained thus causes strain in rings.
Complete answer:
We know that ring strain in organic molecules is a form of instability that exists when the angles formed between the molecules are unstable.
We observe ring strain generally in smaller organic molecules like cyclobutane and cyclopropane.
In the given question, we have that the cyclobutane has an angle strain of ${{9}^{{}^\circ }}{{44}^{'}}$. We know that there are four $C{{H}_{2}}$ groups in cyclobutane and we can draw its structure as-
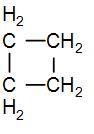
As we can see from the above diagram that there are 4 $C{{H}_{2}}$ groups. So to find the ring strain in cyclobutane, we can subtract the standard enthalpy of combustion of each of these $C{{H}_{2}}$ groups from the standard enthalpy of combustion of cyclobutane.
Therefore, we can write that-
Ring strain = $4\times \Delta H_{c}^{\circ }$ of each $C{{H}_{2}}$ group.-$\Delta H_{c}^{\circ }$of cyclobutane
Therefore, ring strain = $\left( 4\times 660 \right)$KJ/mol - 2274 KJ/mol =140 KJ/mol.
From the above calculation it is clear that ring strain in a cyclobutane ring is 104 KL/mol.
So, the correct answer is “Option B”.
Note: Ring strain is mostly caused due to the $s{{p}^{3}}$ hybridised carbons which are present in the cycloalkanes. For a ring to not be strained the ideal angle is ${{109.5}^{{}^\circ }}$ but due to the $s{{p}^{3}}$ hybridised carbons, the bond angle is not maintained thus causes strain in rings.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Draw the diagram showing the germination of pollen class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

The computer jargonwwww stands for Aworld wide web class 12 physics CBSE




