
What should be the voltage across the resistance R?
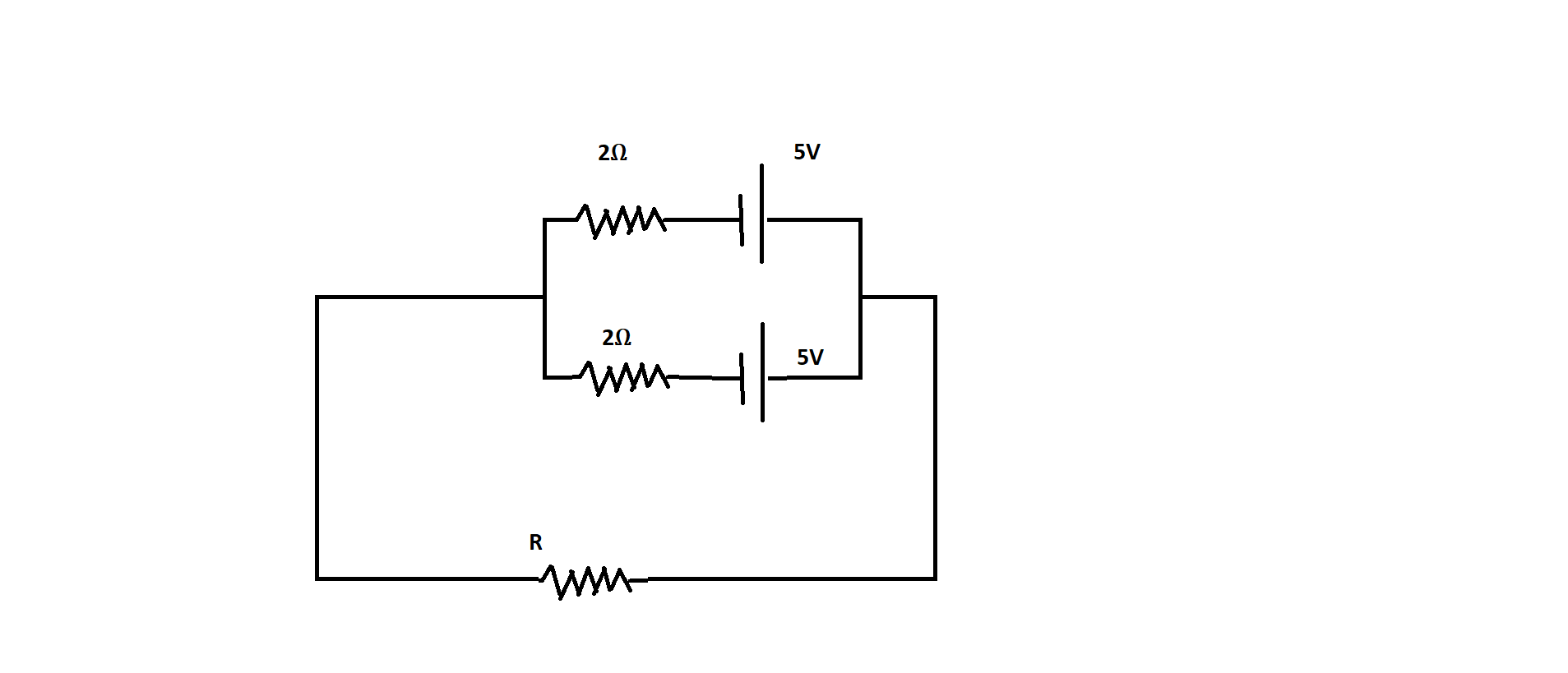
Answer
233.1k+ views
Hint: To solve this question we have to first find the Kirchhoff’s rules of current which states current entering is equal to current leaving. After that, we can use the concept of emf and use the internal resistance of the cell to find the potential drop in the path. With this, we can easily find the voltage across the resistance R.
Formulae used:
$I = {I_1} + {I_2}$
Where $I$ is the total current which is entering, ${I_1}$ is the current across 1st path and ${I_2}$ is the current across 2nd path.
$I = \dfrac{{E - V}}{r}$
Where $I$ is current, $E$ is the Electromotive force (EMF) of the cell, $V$ is the potential drop and $r$ is the internal resistance of the cell.
Complete step by step answer:
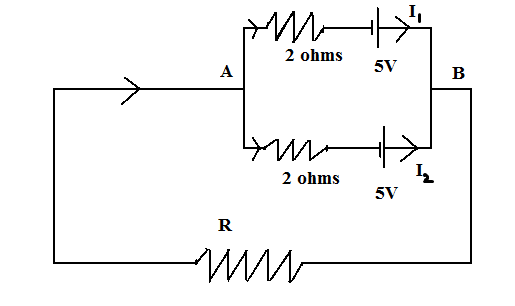
According to Kirchhoff’s law of current, the current entering at point A should be equal to the current leaving at B. So,
$ \Rightarrow I = {I_1} + {I_2}$
Here ${I_1}$ is the current in the path AB upper
And ${I_2}$ is the current in the path AB lower
And $I$ is the current entering through point A
We know that
$I = \dfrac{{E - V}}{r}$
So ${I_1} = \dfrac{{{E_1} - V}}{{{r_1}}}$
Where ${I_1}$ is the current in the upper AB path, ${E_1}$ is the Electromotive force (EMF) of the cell, $V$ is the potential drop and ${r_1}$ is the internal resistance of the cell.
$ \Rightarrow {I_1} = \dfrac{{5 - V}}{2}$
Similarly
${I_2} = \dfrac{{{E_2} - V}}{{{r_2}}}$
Where ${I_2}$ is the current in the upper AB path, ${E_2}$ is the Electromotive force (EMF) of the cell, $V$ is the potential drop and ${r_2}$ is the internal resistance of the cell.
$ \Rightarrow {I_2} = \dfrac{{5 - V}}{2}$
From Kirchhoff’s law of current ,
$I = \dfrac{{5 - V}}{2} + \dfrac{{5 - V}}{2}$
$ \Rightarrow I = 5 - V$
$ \Rightarrow V = 5 - I$
So the required answer is $5 - I$ volts.
Additional information:
Kirchhoff’s law for current conservation and energy conservation is used very commonly to solve questions related to electrical circuits. It can make the calculation of current and voltage in complex cells easy but it works under the assumption that there is no fluctuating magnetic field in the closed-loop. Electric fields and emf could be induced which causes Kirchhoff’s loop rule to break in presence of a variable magnetic field.
Note: Always remember to take care of the direction of current flow. Also, the value of the emf of the cell is important. We should always carefully see if the positive sides i.e., anode, and negative side i.e., cathode are in the same direction or not.
Formulae used:
$I = {I_1} + {I_2}$
Where $I$ is the total current which is entering, ${I_1}$ is the current across 1st path and ${I_2}$ is the current across 2nd path.
$I = \dfrac{{E - V}}{r}$
Where $I$ is current, $E$ is the Electromotive force (EMF) of the cell, $V$ is the potential drop and $r$ is the internal resistance of the cell.
Complete step by step answer:
According to Kirchhoff’s law of current, the current entering at point A should be equal to the current leaving at B. So,
$ \Rightarrow I = {I_1} + {I_2}$
Here ${I_1}$ is the current in the path AB upper
And ${I_2}$ is the current in the path AB lower
And $I$ is the current entering through point A

We know that
$I = \dfrac{{E - V}}{r}$
So ${I_1} = \dfrac{{{E_1} - V}}{{{r_1}}}$
Where ${I_1}$ is the current in the upper AB path, ${E_1}$ is the Electromotive force (EMF) of the cell, $V$ is the potential drop and ${r_1}$ is the internal resistance of the cell.
$ \Rightarrow {I_1} = \dfrac{{5 - V}}{2}$
Similarly
${I_2} = \dfrac{{{E_2} - V}}{{{r_2}}}$
Where ${I_2}$ is the current in the upper AB path, ${E_2}$ is the Electromotive force (EMF) of the cell, $V$ is the potential drop and ${r_2}$ is the internal resistance of the cell.
$ \Rightarrow {I_2} = \dfrac{{5 - V}}{2}$
From Kirchhoff’s law of current ,
$I = \dfrac{{5 - V}}{2} + \dfrac{{5 - V}}{2}$
$ \Rightarrow I = 5 - V$
$ \Rightarrow V = 5 - I$
So the required answer is $5 - I$ volts.
Additional information:
Kirchhoff’s law for current conservation and energy conservation is used very commonly to solve questions related to electrical circuits. It can make the calculation of current and voltage in complex cells easy but it works under the assumption that there is no fluctuating magnetic field in the closed-loop. Electric fields and emf could be induced which causes Kirchhoff’s loop rule to break in presence of a variable magnetic field.
Note: Always remember to take care of the direction of current flow. Also, the value of the emf of the cell is important. We should always carefully see if the positive sides i.e., anode, and negative side i.e., cathode are in the same direction or not.
Recently Updated Pages
JEE Main Mock Test 2025-26: Optics Chapter Practice Online

JEE Main 2025-26 Mock Test: Properties of Solids and Liquids

JEE Main Mock Test 2025-26: Electromagnetic Induction & Alternating Currents

JEE Main 2025-26 Electromagnetic Waves Mock Test with Solutions

JEE Main 2025-26 Mock Test: Electronic Devices Chapter Practice

JEE Main 2025-26 Mock Test: Magnetic Effects of Current & Magnetism

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Understanding Uniform Acceleration in Physics

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Understanding the Electric Field of a Uniformly Charged Ring

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance




