Question

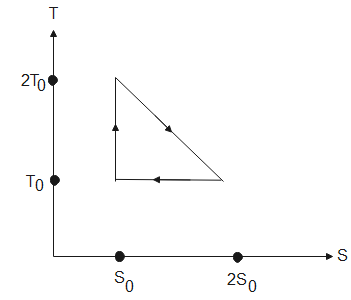
The temperature-entropy diagram of a reversible engine cycle is given in the figure. Its efficiency is

(A). $\dfrac{1}{4}$
(B). $\dfrac{1}{2}$
(C). $\dfrac{2}{3}$
(D). $\dfrac{1}{3}$

Answer 1

Hint: A reversible cycle engine operates between two sources; one at a higher temperature and lower temperature with a working substance. The performance of such engines is determined by the efficiency which depends on the heat absorbed and heat released. The heat changes can be calculated from the graph as area under the curves.
Formula used:
$\eta =1-\dfrac{heat\,lost}{heat\,gained}$
$\eta =1-\dfrac{{{Q}_{2}}}{{{Q}_{1}}}$

Complete answer:
The performance of a reversible engine cycle is determined by the efficiency. It is given by-
$\eta =1-\dfrac{heat\,lost}{heat\,gained}$ - (1)
In a reversible cycle engine, the heat is extracted from a body at lower temperature and given to a body at higher temperature by means of some work.

From the graph, given above, the heat taken or heat given out is calculated by the area under the graph. Therefore, in process 1, the heat absorbed will be-
${{Q}_{1}}=\dfrac{1}{2}{{T}_{0}}{{S}_{0}}+{{T}_{0}}{{S}_{0}}$ [ area of $\Delta =\dfrac{1}{2}bh$, area of a square= $s\times s$]
$\Rightarrow {{Q}_{1}}=\dfrac{3}{2}{{T}_{0}}{{S}_{0}}$
Therefore, the heat absorbed in the reversible engine cycle is $\dfrac{3}{2}{{T}_{0}}{{S}_{0}}$
In process 2, the heat released is given by-
${{Q}_{2}}={{T}_{0}}{{S}_{0}}$
The heat released in process 2 is ${{T}_{0}}{{S}_{0}}$.
In process 3, the area covered under the graph is zero, hence no heat is absorbed or released in this process.
From eq (1), the efficiency of the engine will be-
$\eta =1-\dfrac{{{Q}_{2}}}{{{Q}_{1}}}$
Therefore, we substitute values in the above equation to get,
$\begin{align}
  & \eta =1-\dfrac{{{T}_{0}}{{S}_{0}}}{\dfrac{3}{2}{{T}_{0}}{{S}_{0}}} \\
 & \Rightarrow \eta =1-\dfrac{2}{3} \\
 & \therefore \eta =\dfrac{1}{3} \\
\end{align}$
The efficiency of the engine is $\dfrac{1}{3}$.
Therefore, the efficiency of the reversible cycle engine is $\dfrac{1}{3}$.

Hence, the correct option is (D).

Note:
For all reversible cycle engines acting between two same temperatures, the Carnot engine has the highest efficiency. The efficiency can also be calculated as the ratio of heat absorbed to the work done. The performance of reversible engines is commonly calculated by the coefficient of performance.