Question

The range of the ammeter is 5 amperes, and the full-scale deflection current is 0.5 micro-amperes. If the resistance of the galvanometer is 50 ohms, then find the shunt resistance.

Answer 1

Hint: In this question, we need to determine the value of the shunt resistance that should be attached in parallel with the 50 ohms resistance such that the full-scale deflection of the ammeter is 0.5 micro-amperes whereas the total range of the ammeter is 5 Amperes. For this, we will use the relations for Kirchhoff’s law.

Complete step by step answer:The internal resistance of the ammeter is connected in series, and to extend the range of the ammeter, an additional resistance should be connected in parallel with the internal resistance. The resistances connected in parallel are known as Shunt resistances.
Here, the full-scale deflection is $0.5\mu A$ , and the range is 5 Amperes so, the current passing through the shunt resistance is $\left( {5 - 0.5 \times {{10}^{ - 6}}} \right) = 4.9999995A$

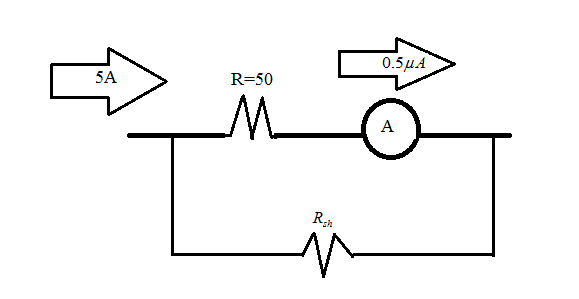
As we know, the potential drop across the resistances connected in parallel is the same. SO,
$
  {V_g} = {V_{sh}} \\
  \left( {0.5\mu A} \right)\left( {50} \right) = \left( {4.9999995} \right)\left( {{R_{sh}}} \right) \\
  {R_{sh}} = \dfrac{{50 \times 0.5 \times {{10}^{ - 6}}}}{{4.9999995}} \\
   = 5\mu \Omega \\
 $
Hence, the value of the shunt resistance that should be connected in parallel with the ammeter is 5 micro-ohms.

Note:It is interesting to note here that as we need to increase the range of the ammeter so we have connected a very low value of the resistance so that a major part of the current inline will flow through it without harming the meter.