Questions & Answers
Question
Answers
Related Questions
The number of neighbours around each particle in a face-centred cubic lattice is:
A.4
B.6
C.12
D.8
Answer
![Verified]()
Verified
Verified
Hint:
In a face centred cubic (fcc) lattice, the atoms of the given substance are located on all 6 sides of the cubic structure as well as on all the 8 vertices of the cube.
Complete step by step answer:
The geometrical representation or the structure of a face centred cubic lattice can be visually represented as follows:
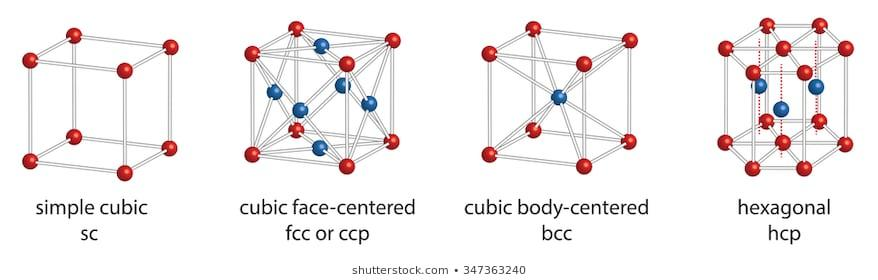
As the name suggests, a Face Centred Cubic (fcc) lattice structure has atoms on all the sides of the cubic structure as well as all the vertices. There is no atom present in the centre of the cube. This brings the total count of the total number of atoms present in a Face Centred Cubic structure to 12. Considering that each vertex contains \[{\dfrac{1}{8}^{th}}\]of an atom and each face contains half an atom, the total number of atoms present in face centred cubic lattice is :
= \[\dfrac{1}{8}\](number of vertices) + \[\dfrac{1}{2}\](number of sides)
= \[\dfrac{1}{8}\](8) + \[\dfrac{1}{2}\](6)
\[ = {\text{ }}1{\text{ }} + {\text{ }}3\]
\[ = {\text{ }}4 \]atoms
Hence in FCC, there are 4 atoms per unit cell.
-In order to understand the number of neighbours around each particle in a face-centred cubic, we must understand a concept known as Coordination number.
-In chemistry, crystallography, and materials science, the coordination number, also called ligancy, of a central atom in a molecule or crystal is the number of atoms, molecules or ions bonded to it.
-The coordination number is fixed for a certain type of lattice structure. And for Face Centred Cubic lattice structure, the coordination number is 12.
-Hence, by definition, the number of neighbours around each particle in a face-centred cubic lattice is 12.
Hence, Option C is the correct option.
Note:
The coordination number for the various types of cubic arrangements are as follows:
Simple cubic lattice: 6
Body centred cubic lattice: 8
Face centred cubic lattice: 12
In a face centred cubic (fcc) lattice, the atoms of the given substance are located on all 6 sides of the cubic structure as well as on all the 8 vertices of the cube.
Complete step by step answer:
The geometrical representation or the structure of a face centred cubic lattice can be visually represented as follows:
As the name suggests, a Face Centred Cubic (fcc) lattice structure has atoms on all the sides of the cubic structure as well as all the vertices. There is no atom present in the centre of the cube. This brings the total count of the total number of atoms present in a Face Centred Cubic structure to 12. Considering that each vertex contains \[{\dfrac{1}{8}^{th}}\]of an atom and each face contains half an atom, the total number of atoms present in face centred cubic lattice is :
= \[\dfrac{1}{8}\](number of vertices) + \[\dfrac{1}{2}\](number of sides)
= \[\dfrac{1}{8}\](8) + \[\dfrac{1}{2}\](6)
\[ = {\text{ }}1{\text{ }} + {\text{ }}3\]
\[ = {\text{ }}4 \]atoms
Hence in FCC, there are 4 atoms per unit cell.
-In order to understand the number of neighbours around each particle in a face-centred cubic, we must understand a concept known as Coordination number.
-In chemistry, crystallography, and materials science, the coordination number, also called ligancy, of a central atom in a molecule or crystal is the number of atoms, molecules or ions bonded to it.
-The coordination number is fixed for a certain type of lattice structure. And for Face Centred Cubic lattice structure, the coordination number is 12.
-Hence, by definition, the number of neighbours around each particle in a face-centred cubic lattice is 12.
Hence, Option C is the correct option.
Note:
The coordination number for the various types of cubic arrangements are as follows:
Simple cubic lattice: 6
Body centred cubic lattice: 8
Face centred cubic lattice: 12
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
-
NEET
-
NEET 2021
-
NEET 2022
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Class 9
-
Class 10
-
-
Micro Courses
-
-
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
