Question

The moment of inertia of an uniform thin sheet of mass M of the given shape about the specified axis is (axis and sheet both are in same plane):

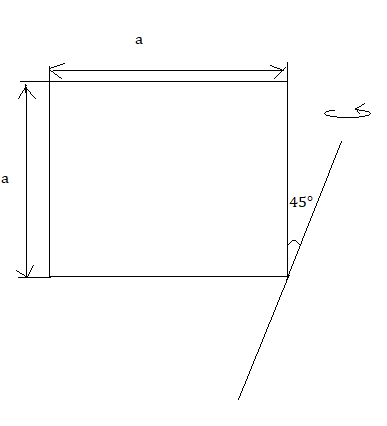
A. \[\dfrac{7}{2}M{{a}^{2}}\]
B. \[\dfrac{5}{12}M{{a}^{2}}\]
C. \[\dfrac{1}{3}M{{a}^{2}}\]
D. \[\dfrac{1}{12}M{{a}^{2}}\]

Answer 1

Hint: The moment of Inertia is denoted by I, measures the extent to which an object resists rotational acceleration about a particular axis, and is the rotational analogue to mass. Mass moments of inertia have units of dimension = ML$^2$ ([mass] × [length]$^2$).
The moment of the inertia of the sheet with respect to an axis perpendicular to the plane is
 $I=\dfrac{1}{6}M{{a}^{2}}$.

Formula used: \[I={{I}_{1}}+{{I}_{2}}\] (perpendicular axis theorem) and \[{{I}_{2}}={{I}_{1}}+M{{d}^{2}}\] (parallel axis theorem).

Complete step by step solution:
The moment of the inertia of the sheet with respect to an axis perpendicular to the plane is: -
$I=\dfrac{1}{6}M{{a}^{2}}$.
Let the moment of inertia of the diagonals of the sheets be I1 and I2 then according to perpendicular axis theorem, \[I={{I}_{1}}+{{I}_{2}}\]
By symmetry, \[{{I}_{1}}={{I}_{2}}=2I\]
\[{{I}_{1}}=\dfrac{1}{12}M{{a}^{2}}\]

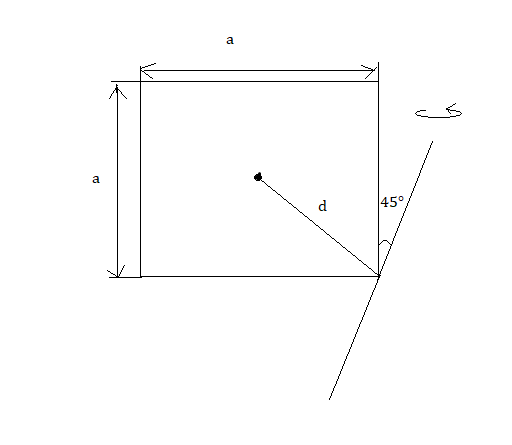
Now, using the parallel axis theorem, the moment of inertia of the given axis [i.e.,45${}^\circ $ to the side] is,
\[{{I}_{2}}={{I}_{1}}+M{{d}^{2}}\]
 [where, $d=\dfrac{a\sqrt{2}}{2}$ as shown in the figure beside]
\[\begin{align}
  & {{I}_{2}}=\dfrac{1}{12}M{{a}^{2}}+\dfrac{2}{4}M{{a}^{2}} \\
 & {{I}_{2}}=\dfrac{M{{a}^{2}}+6M{{a}^{2}}}{12} \\
 & {{I}_{2}}=\dfrac{7M{{a}^{2}}}{12} \\
\end{align}\]
Thus, option A is the correct answer.

Additional information: For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. Typically this occurs when the mass density is constant, but in some cases the density can vary throughout the object as well. In general, it may not be straightforward to symbolically express the moment of inertia of shapes with more complicated mass distributions and lacking symmetry. When calculating moments of inertia, it is useful to remember that it is an additive function and exploit the parallel axis and theorems. This article mainly considers symmetric mass distributions, with constant density throughout the object, and the axis of rotation is taken to be through the centre of mass unless otherwise specified.

Note: Moment of Inertia for different shapes can be found out from the perpendicular axis theorem and the parallel axis theorem. In general, the moment of inertia is a tensor.