Question

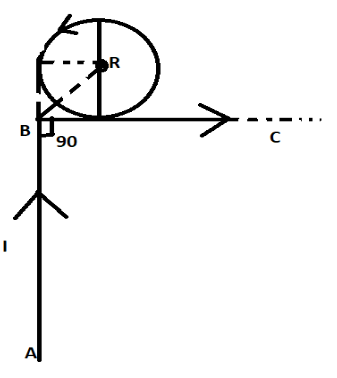
The magnetic field at the center of the circular loop as shown in the figure, when the single wire is bent to form a circular loop and also extends to form a straight section is:
A. $\dfrac{{{\mu _0}I}}{{2R}} \odot $
B. $\dfrac{{{\mu _0}I}}{{2R}}\left( {1 + \dfrac{1}{{\pi \sqrt 2 }}} \right) \odot $
C. $\dfrac{{{\mu _0}I}}{{2R}}\left( {1 - \dfrac{1}{{\pi \sqrt 2 }}} \right) \otimes $
D. $\dfrac{{{\mu _0}I}}{R}\left( {1 - \dfrac{1}{{\pi \sqrt 2 }}} \right) \otimes $

Answer 1

Hint:In the above question, we have to find the total magnetic field. Then firstly, finding the magnetic field along the straight wire and then extending the circular loop and then again, the magnetic field of the straight wire. After adding all the magnetic fields, we got the final answer.

Complete step by step answer:
The total magnetic field will be given by adding the magnetic field of straight line and the magnetic field of the circular loop and again the magnetic field of straight line.Magnetic field can be calculated by the Biot savart’s law whose expression be given by,
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idr \times r}}{{{r^3}}}$
Magnetic field of straight wire be given by the formula,
$B = \dfrac{{{\mu _0}I}}{{4\pi r}}\left( {sin{\theta _1} + \sin {\theta _2}} \right)$
where ${\theta _{1,}}{\theta _2}$ are the angles corresponding to the two ends of the wire.
Now, the magnetic field along AB,
$
{B_1} = \dfrac{{{\mu _0}I}}{{4\pi R}}\left( {sin\dfrac{\pi }{2} - \sin \dfrac{\pi }{4}} \right) \otimes \\
\Rightarrow{B_1} = \dfrac{{{\mu _0}I}}{{4\pi R}}\left( {1 - \dfrac{1}{{\sqrt 2 }}} \right) \otimes \\
$ $ \ldots \ldots \left( 1 \right)$
Now, the magnetic field along the circular loop
${B_2} = \dfrac{{{\mu _0}I}}{{2R}} \odot $ $ \ldots \ldots \left( 2 \right)$
Magnetic field along the wire BC,
$
{B_3} = \dfrac{{\mu {}_0I}}{{4\pi R}}\left( {\sin \dfrac{\pi }{2} + \sin \dfrac{\pi }{4}} \right) \odot \\
\Rightarrow{B_3} = \dfrac{{{\mu _0}I}}{{4\pi R}}\left( {1 + \dfrac{1}{{\sqrt 2 }}} \right) \odot \\
$ $ \ldots \ldots \left( 3 \right)$
Now adding all the above marked equations:
$\overrightarrow B = {B_1} + {B_2} + {B_3}$
$
\Rightarrow\overrightarrow B = \left( {\dfrac{{{\mu _0}I}}{{2R}} + \dfrac{{2{\mu _0}I}}{{4\pi R}}\dfrac{1}{{\sqrt 2 }}} \right) \odot \\
\therefore\overrightarrow B = \dfrac{{{\mu _0}I}}{{2R}}\left( {1 + \dfrac{1}{{\pi \sqrt 2 }}} \right) \odot \\ $
Hence, the correct option is B.

Note:The value of proportionality is $\dfrac{{{\mu _0}}}{{4\pi }} = {10^{ - 7}}N{A^{ - 2}}$.Biot savart law is a vector quantity which contains both magnitude and direction.$ \otimes $ is the inward direction of the field and $ \odot $ is the outward direction of the field.