
The locus of the foot of the perpendicular from the origin on each member of the family \[(4a+3)x-(a+1)y-(2a+1)=0\] is
(a). \[{{(2x-1)}^{2}}+4{{(y+1)}^{2}}=5\]
(b). \[{{(2x-1)}^{2}}+{{(y+1)}^{2}}=5\]
(c). \[{{(2x+1)}^{2}}+4{{(y-1)}^{2}}=5\]
(d). \[{{(2x-1)}^{2}}+4{{(y-1)}^{2}}=5\]
Answer
219.3k+ views
Hint:- In this question first we have to find the value of the point of intersection of the family of straight lines then apply Pythagoras theorem to get the required answer.
Complete step-by-step solution -
The equation of the family of lines is,
\[(4a+3)x-(a+1)y-(2a+1)=0\]
Expanding this, we get
\[4ax+3x-ay-y-2a-1=0\]
Now regrouping them, we get
\[3x-y-1+a(4x-y-2)=0\]
Now this is of the form \[{{L}_{1}}+\lambda {{L}_{2}}=0\].
Let the point of intersection of these two lines, i.e., \[3x-y-1=0\]and \[4x-y-2=0\]be P.
So, the given family of lines will pass through this fixed point P, as shown below.
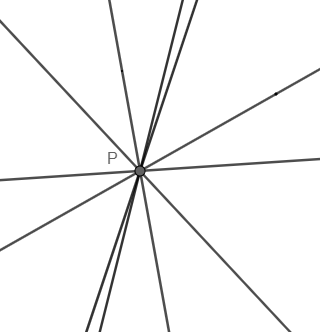
Now we will find the coordinates of point P.
Consider,
\[3x-y-1=0\]
\[3x=y+1\]
\[x=\dfrac{y+1}{3}........(i)\]
Substitute this value in other equation of line, we get
\[4x-y-2=0\]
\[4\left( \dfrac{y+1}{3} \right)-y-2=0\]
\[\dfrac{4y+4-3y-(3\times 2)}{3}=0\]
\[y+4-6=0\]
\[y=6-4=2\]
Substituting the value of ‘y’ in equation (i), we get
\[x=\dfrac{2+1}{3}=\dfrac{3}{3}=1\]
So, the point of intersection of the family of lines is \[P(1,2)\].
Now, there is a perpendicular drawn from the origin onto each line. Let the foot of the perpendicular on each line be \[A(x,y)\], as shown below.
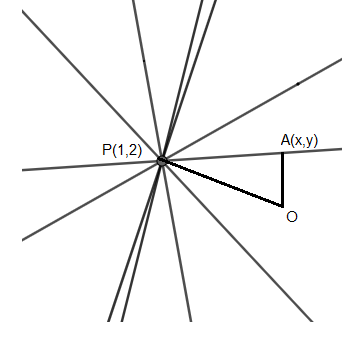
Now the points OPA will form a right-angled triangle in all the lines.
Applying Pythagoras theorem on \[\Delta OPA\], we get
\[O{{P}^{2}}=O{{A}^{2}}+A{{P}^{2}}.........(ii)\]
We know the distance between points \[({{x}_{1}},{{y}_{1}})\]and \[({{x}_{2}},{{y}_{2}})\]is given by the distance formula, i.e.,
\[\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]
Applying the distance formula in equation (ii), we get
\[{{\left( \sqrt{{{(1-0)}^{2}}+{{(2-0)}^{2}}} \right)}^{2}}={{\left( \sqrt{{{(x-0)}^{2}}+{{(y-0)}^{2}}} \right)}^{2}}+{{\left( \sqrt{{{(x-1)}^{2}}+{{(y-2)}^{2}}} \right)}^{2}}\]
\[{{1}^{2}}+{{2}^{2}}={{x}^{2}}+{{y}^{2}}+{{(x-1)}^{2}}+{{(y-2)}^{2}}\]
Expanding, we get
\[1+4={{x}^{2}}+{{y}^{2}}+({{x}^{2}}+1-2x)+({{y}^{2}}+4-4y)\]
\[5=2{{x}^{2}}+2{{y}^{2}}+1-2x+4-4y\]
As this is not matching with the options, we will multiply the above equation with \[2\], we get
\[10=4{{x}^{2}}+4{{y}^{2}}+2-4x+8-8y\]
Grouping them, we get
\[4{{x}^{2}}-4x+2+4{{y}^{2}}-8y+8=10\]
Now we will try to convert this into \[{{(a+b)}^{2}}\]form, as in options.
\[\left( 4{{x}^{2}}-4x+1 \right)+1+4({{y}^{2}}-2y+1)+4=10\]
We know, \[\left( {{a}^{2}}-2ab+{{b}^{2}} \right)={{(a+b)}^{2}}\], so above equation can be re-written as,
\[{{\left( 2x-1 \right)}^{2}}+4{{(y-1)}^{2}}=10-4-1\]
\[{{\left( 2x-1 \right)}^{2}}+4{{(y-1)}^{2}}=5\]
So, the locus of the foot of the perpendicular from the origin on each member of the family \[(4a+3)x-(a+1)y-(2a+1)=0\] is \[{{\left( 2x-1 \right)}^{2}}+4{{(y-1)}^{2}}=5\].
Hence, the correct answer is option (d).
Note: Another method to find the answer is, instead of using Pythagoras theorem; we can find the slope of the equation of perpendicular line from the origin to a point. Then applying the formula, $y=mx+c$. But this would be a lengthy process.
Complete step-by-step solution -
The equation of the family of lines is,
\[(4a+3)x-(a+1)y-(2a+1)=0\]
Expanding this, we get
\[4ax+3x-ay-y-2a-1=0\]
Now regrouping them, we get
\[3x-y-1+a(4x-y-2)=0\]
Now this is of the form \[{{L}_{1}}+\lambda {{L}_{2}}=0\].
Let the point of intersection of these two lines, i.e., \[3x-y-1=0\]and \[4x-y-2=0\]be P.
So, the given family of lines will pass through this fixed point P, as shown below.

Now we will find the coordinates of point P.
Consider,
\[3x-y-1=0\]
\[3x=y+1\]
\[x=\dfrac{y+1}{3}........(i)\]
Substitute this value in other equation of line, we get
\[4x-y-2=0\]
\[4\left( \dfrac{y+1}{3} \right)-y-2=0\]
\[\dfrac{4y+4-3y-(3\times 2)}{3}=0\]
\[y+4-6=0\]
\[y=6-4=2\]
Substituting the value of ‘y’ in equation (i), we get
\[x=\dfrac{2+1}{3}=\dfrac{3}{3}=1\]
So, the point of intersection of the family of lines is \[P(1,2)\].
Now, there is a perpendicular drawn from the origin onto each line. Let the foot of the perpendicular on each line be \[A(x,y)\], as shown below.

Now the points OPA will form a right-angled triangle in all the lines.
Applying Pythagoras theorem on \[\Delta OPA\], we get
\[O{{P}^{2}}=O{{A}^{2}}+A{{P}^{2}}.........(ii)\]
We know the distance between points \[({{x}_{1}},{{y}_{1}})\]and \[({{x}_{2}},{{y}_{2}})\]is given by the distance formula, i.e.,
\[\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]
Applying the distance formula in equation (ii), we get
\[{{\left( \sqrt{{{(1-0)}^{2}}+{{(2-0)}^{2}}} \right)}^{2}}={{\left( \sqrt{{{(x-0)}^{2}}+{{(y-0)}^{2}}} \right)}^{2}}+{{\left( \sqrt{{{(x-1)}^{2}}+{{(y-2)}^{2}}} \right)}^{2}}\]
\[{{1}^{2}}+{{2}^{2}}={{x}^{2}}+{{y}^{2}}+{{(x-1)}^{2}}+{{(y-2)}^{2}}\]
Expanding, we get
\[1+4={{x}^{2}}+{{y}^{2}}+({{x}^{2}}+1-2x)+({{y}^{2}}+4-4y)\]
\[5=2{{x}^{2}}+2{{y}^{2}}+1-2x+4-4y\]
As this is not matching with the options, we will multiply the above equation with \[2\], we get
\[10=4{{x}^{2}}+4{{y}^{2}}+2-4x+8-8y\]
Grouping them, we get
\[4{{x}^{2}}-4x+2+4{{y}^{2}}-8y+8=10\]
Now we will try to convert this into \[{{(a+b)}^{2}}\]form, as in options.
\[\left( 4{{x}^{2}}-4x+1 \right)+1+4({{y}^{2}}-2y+1)+4=10\]
We know, \[\left( {{a}^{2}}-2ab+{{b}^{2}} \right)={{(a+b)}^{2}}\], so above equation can be re-written as,
\[{{\left( 2x-1 \right)}^{2}}+4{{(y-1)}^{2}}=10-4-1\]
\[{{\left( 2x-1 \right)}^{2}}+4{{(y-1)}^{2}}=5\]
So, the locus of the foot of the perpendicular from the origin on each member of the family \[(4a+3)x-(a+1)y-(2a+1)=0\] is \[{{\left( 2x-1 \right)}^{2}}+4{{(y-1)}^{2}}=5\].
Hence, the correct answer is option (d).
Note: Another method to find the answer is, instead of using Pythagoras theorem; we can find the slope of the equation of perpendicular line from the origin to a point. Then applying the formula, $y=mx+c$. But this would be a lengthy process.
Recently Updated Pages
Chemical Equation - Important Concepts and Tips for JEE

JEE Main 2022 (July 29th Shift 1) Chemistry Question Paper with Answer Key

Conduction Explained: Definition, Examples & Science for Students

Analytical Method of Vector Addition Explained Simply

Atomic Size - Important Concepts and Tips for JEE

JEE Main 2022 (June 29th Shift 1) Maths Question Paper with Answer Key

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

NCERT Solutions For Class 11 Maths Chapter 8 Sequences And Series

How to Convert a Galvanometer into an Ammeter or Voltmeter

NCERT Solutions For Class 11 Maths Chapter 12 Limits And Derivatives




