Question

The length of a focal chord of the parabola \[{{y}^{2}}=4ax\] making an angle with the axis of the parabola is
a) $ 4\text{a cose}{{\text{c}}^{2}}\text{ }\!\!\theta\!\!\text{ } $
b) $ 4\text{a se}{{\text{c}}^{2}}\text{ }\!\!\theta\!\!\text{ } $
c) $ \text{a cose}{{\text{c}}^{2}}\text{ }\!\!\theta\!\!\text{ } $
d) None of these

Answer 1

Hint: For the given parabola \[{{y}^{2}}=4ax\], the axis of symmetry is y-axis and the focus lie on $ (a,0) $ .
The focal chord is a line segment that passes through the focus of the parabola and has its end points at the parabola. Let us assume that PQ is the focal chord of the given parabola. Consider \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[Q\left( at_{2}^{2},2a{{t}_{2}} \right)\] be the end points of a focal chord of parabola. So, to find the distance of focal chord use the distance formula:
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}\]

Complete step-by-step answer:
To find a relation between $ {{t}_{1}} $ and $ {{t}_{2}} $ , we can use the slope of a line which is given as:
\[\text{tan }\!\!\theta\!\!\text{ }=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
Get the relation between $ {{t}_{1}} $ and $ {{t}_{2}} $ , and substitute in the distance formula to get the length of the focal chord.
The below diagram shows the given parabola \[{{y}^{2}}=4ax\] with focus at $ F(a,0) $ . Let us assume that PQ is the focal chord of the given parabola \[{{y}^{2}}=4ax\]. Consider \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[Q\left( at_{2}^{2},2a{{t}_{2}} \right)\] be the end points of a focal chord of parabola

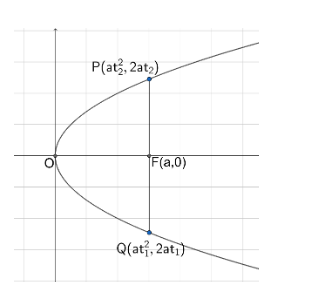
Let us assume that PQ is the focal chord of the given parabola. Consider \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[Q\left( at_{2}^{2},2a{{t}_{2}} \right)\] be the end points of a focal chord of parabola.
Since PQ is the focal chord, therefore, $ {{t}_{1}}\times {{t}_{2}}=-1 $
So, by using distance formula: \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}\]
we get the length of focal chord of parabola as:
\[\begin{align}
  & PQ=\sqrt{{{\left( at_{2}^{2}-at_{1}^{2} \right)}^{2}}+{{\left( 2a{{t}_{2}}-2a{{t}_{1}} \right)}^{2}}} \\
 & =\sqrt{{{a}^{2}}{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}{{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4{{a}^{2}}{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}} \\
 & =a\left( {{t}_{2}}-{{t}_{1}} \right)\sqrt{{{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4} \\
 & =a\sqrt{\left( {{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4 \right){{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}}......(1)
\end{align}\]

By using identity $ {{\left( a+b \right)}^{2}}-4ab={{\left( a-b \right)}^{2}} $
We can write equation (1) as:
\[PQ=a\sqrt{\left( {{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4 \right)\left( {{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}-4 \right)}......(2)\]
Since $ {{t}_{1}}\times {{t}_{2}}=-1 $
By substituting the value of $ {{t}_{1}}\times {{t}_{2}}=-1 $ in equation (2), we get:
\[\begin{align}
  & PQ=a\sqrt{\left( {{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4 \right)\left( {{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}-4\left( -1 \right) \right)} \\
 & =a\sqrt{\left( {{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4 \right)\left( {{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4 \right)} \\
 & =a\sqrt{{{\left( {{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4 \right)}^{2}}} \\
 & =a\left( {{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4 \right)......(3)
\end{align}\]

Let us assume that PQ makes and angle \[\text{ }\!\!\theta\!\!\text{ }\] with x-axis.
The slope of any line can be given as: \[\text{tan }\!\!\theta\!\!\text{ }=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
Therefore, the slope of the focal chord PQ can be written as:
\[\begin{align}
  & \text{tan }\!\!\theta\!\!\text{ }=\dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{at_{2}^{2}-at_{1}^{2}} \\
 & =\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( t_{2}^{2}-t_{1}^{2} \right)} \\
 & =\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( t_{2}^{2}-t_{1}^{2} \right)}......(4)
\end{align}\]
Now, simplify the equation (4), by using the identity:
\[\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a-b \right)\left( a+b \right)\]
we get:
\[\begin{align}
  & \text{tan }\!\!\theta\!\!\text{ }=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)} \\
 & \Rightarrow \text{tan }\!\!\theta\!\!\text{ }=\dfrac{2}{\left( {{t}_{2}}+{{t}_{1}} \right)} \\
 & \Rightarrow \left( {{t}_{2}}+{{t}_{1}} \right)=\dfrac{1}{\text{tan }\!\!\theta\!\!\text{ }}......(5) \\
\end{align}\]
Since \[\dfrac{1}{\text{tan }\!\!\theta\!\!\text{ }}=\text{cot }\!\!\theta\!\!\text{ }\]
Therefore, we can write equation (5) as:
 $ \Rightarrow \left( {{t}_{2}}+{{t}_{1}} \right)=\cot \text{ }\!\!\theta\!\!\text{ } $
Substitute the value of \[\left( {{t}_{2}}+{{t}_{1}} \right)\] in equation (3) we get:
\[\begin{align}
  & PQ=a\left( {{\left( \text{2cot }\!\!\theta\!\!\text{ } \right)}^{2}}+4 \right) \\
 & =a\left( 4{{\cot }^{2}}\text{ }\!\!\theta\!\!\text{ + 4} \right) \\
 & =4a\left( {{\cot }^{2}}\text{ }\!\!\theta\!\!\text{ + 1} \right)
\end{align}\]
Since $ \left( 1+{{\cot }^{2}}\text{ }\!\!\theta\!\!\text{ } \right)=\text{cose}{{\text{c}}^{2}}\text{ }\!\!\theta\!\!\text{ } $
Hence, $ PQ=4a\text{ cose}{{\text{c}}^{2}}\text{ }\!\!\theta\!\!\text{ } $
So, the correct answer is “Option A”.

Note: Be careful while identifying the axis of symmetry as well as the focus of the given parabola. The choice of coordinates of endpoints of the focal chord is necessary to keep in mind because the distance of PQ is dependent on the coordinates of endpoints. Also, while finding the slope of the focal chord, one should substitute the values in the right place.