Question

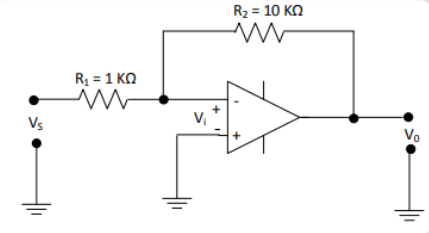
The inverting op-amp shown in the figure has an open-loop gain of 100. The closed-loop gain $\dfrac{{{V_0}}}{{{V_s}}}$ is
 

A) -8
B) -9
C) -10
D) -11

Answer 1

Hint: The amplifier is a circuit that can amplify the given input signals and hence make the signal suitable for transmission and processing. The transistor amplifiers can be classified as common emitter, common base, and common collector. The common emitter amplifier is the one with the emitter connected to the ground.

Complete step by step solution:
An amplifier is a generic term used to describe a circuit that produces an increased version of its input signal, or we can say that the circuit or device can amplify the given input signal. What is the need for the amplifier? We have many signals from nature which we sense using the sensors. But these signals are very low in strength when we cannot directly use them for analysis and transmission. So we need to amplify the signal transmission and processing. For this process, we need the amplifiers to amplify or to increase the strength of the signals.

Given:
${R_1} = 1\;{\rm{k\Omega }}$
${R_2} = 10\;{\rm{k\Omega }}$
Open-loop gain is ${A_{OL}} = 100$
We will now write the formula for the closed-loop gain ${A_r}$ for inverting op-amp.
${A_r} = \dfrac{{{V_0}}}{{{V_s}}} = \dfrac{{\dfrac{{ - {R_2}}}{{{R_1}}}}}{{1 + \left( {\dfrac{{1 + \dfrac{{{R_2}}}{{{R_1}}}}}{{{A_{OL}}}}} \right)}}$
Here ${V_0}$ and ${V_s}$ are the output and supply voltage. We can rewrite the above equation as,
$\dfrac{{{V_0}}}{{{V_s}}} = \dfrac{{\dfrac{{ - {R_2}}}{{{R_1}}}}}{{1 + \left( {\dfrac{{1 + \dfrac{{{R_2}}}{{{R_1}}}}}{{{A_{OL}}}}} \right)}}$
We will now substitute ${R_1} = 1\;{\rm{k\Omega }}$ , ${R_2} = 10\;{\rm{k\Omega }}$ ${A_{OL}} = 100$ to find the value of closed-loop gain.
$\dfrac{{{V_0}}}{{{V_s}}} = \dfrac{{\dfrac{{ - 10\;\Omega }}{{1\;\Omega }}}}{{1 + \left( {\dfrac{{1 + \dfrac{{10\;\Omega }}{{1\;\Omega }}}}{{100}}} \right)}}$
$\dfrac{{{V_0}}}{{{V_s}}} = \dfrac{{ - 10\;\Omega }}{{1 + \left( {\dfrac{{11\;\Omega }}{{100}}} \right)}}$
$\dfrac{{{V_0}}}{{{V_s}}} = \dfrac{{ - 10 \times 100}}{{111}}$
$\dfrac{{{V_0}}}{{{V_s}}} = - 9.009$

Therefore, the closed-loop gain is -9.009, and the correct option is (B).

Hint: An Operating Amplifier is effectively a three-terminal unit containing two high impedance inputs. Each of the inputs is called the Inverting Input. Another input is termed as non-inverting Input, labeled with a positive sign. A summing amplifier with multiple resistors at the inputs produces a weighted sum. This is used in a digital-to-analog converter to transform a binary number to a voltage. A summing amplifier is used in conjunction with an AC signal voltage to add a DC offset voltage.