Question

The intensity of an electric field inside a capacitor is $ E $ . The work required to make a charge $ q $ move in a closed rectangular circuit is?

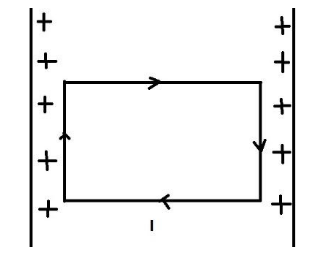
(A) $ 2\left( {l + b} \right)qE $
(B) $ 2lbqE $
(C) $ 2bqE $
(D) Zero

Answer 1

Hint: The work done in taking a charge between two points in an electric field generated by fixed charges is independent of the path taken between the points. This is because the electric field is perpendicular to the displacement.

Formula Used: The formulae used in the solution are given here.
Electric field $ E = \dfrac{F}{q} $ where $ F $ is the force and $ q $ is the charge.
Potential difference $ V = E.d $ where $ E $ is the electric field and $ d $ is the distance between points the potential difference is measured.

Complete Step by Step Solution
The electric field can be defined as a vector field which describes the relationship between the charge of a test particle introduced in the field and the force exerted upon this charged test particle.
Electric field $ E = \dfrac{F}{q} $ where $ F $ is the force and $ q $ is the charge.
Capacitors are devices which store electrical potential energy using an electric field. As such, capacitors are governed by the rules of electromagnetism.
Force is given by, $ F = qE $ .
The work done in taking a charge between two points in an electric field generated by fixed charges is independent of the path taken between the points. An equipotential surface is one in which all the points are at the same electric potential. If a charge is to be moved between any two points (say from point A to point B) on an equipotential surface, according to the formula $ dW = q.dVdW = q.dV $ , the work done becomes zero.
For a capacitor, electric field intensity is $ E $ , a charge $ q $ moves in a closed rectangular circuit.

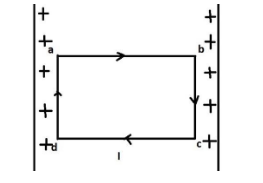
Here, abcda is a rectangular loop placed in the electric field $ E $ . As ab = cd = $ l $ = length of loop and bc =da = $ b $ = breadth of loop.
Then, potential difference across ab, $ {V_{ab}} = El $
Potential difference across cd, $ {V_{cd}} = - El $
Similarly, Potential difference across bc, $ {V_{bc}} = 0 $ [position vector is perpendicular on electric field lines]
Potential difference across cd, $ {V_{cd}} = - El $
Now, work done by moving charge q over a closed rectangular loop abcda is equal to,
 $ q\left( {{V_{ab}} + {V_{cd}} + {V_{bc}} + {V_{da}}} \right) $
 $ = q\left( {El - El + 0 + 0} \right) = 0 $
Hence, work done by moving point charge q over the closed rectangular loop abcda is zero.
So the correct answer is option D.

Note
Electric potential, also called the electric field potential, is the amount of electric potential energy that a charged particle would have at a certain point in space. The voltage, also called potential difference between two points in space is the difference of the electric potentials of those two points. The unit used for electric potential is a volt [ $ V $ ], named after the Italian physicist Alessandro Volta. The same unit is used for voltage. The electric potential between two points in an uniform field is the negative of the field intensity difference between those two points.