Question

The distance between the slits in a Young’s double slit experiment is $ d $ and the distance of the screen from the plane of the slits is $ b $ . P is a point on the screen directly in front of one of the slits. The path difference between the waves arriving at P from the two slits is
(A) $ \dfrac{{{d^2}}}{b} $
(B) $ \dfrac{{{d^2}}}{{2b}} $
(C) $ \dfrac{{2{d^2}}}{b} $
(D) $ \dfrac{{{d^2}}}{{4b}} $

Answer 1

Hint To solve this question, we need to use the formula for the path difference between two rays emerging from the two slits for the Young’s double slit experiment. By putting the required values from the conditions given in the question into the formula we will get the final answer.

Formula Used: The formula which is used in solving the above question is given by
 $ x = \dfrac{{yd}}{D} $ , here $ x $ is the path difference between the rays coming from the two slits of width $ d $ at the point situated at the distance of $ y $ from the centre of the slits on the screen at a distance of $ D $ from the plane of the slits.

Complete step by step answer
We represent the situation given in the question by the below diagram.

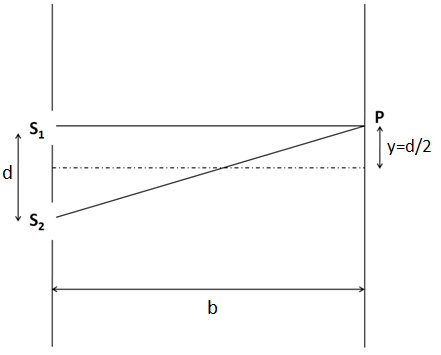
Since the point P is situated in front of one of the two slits, so we take it to be in from of the upper slit $ {S_1} $ . So, the distance of the point P from the centre of the slit becomes
 $ y = \dfrac{d}{2} $ (1)
The two rays originating from the slits meet at the point P. From the above figure, this path difference is given by
 $ x = {S_2}P - {S_1}P $
Now, we know that the path difference in the Young’s double slit experiment is given by
 $ x = \dfrac{{yd}}{D} $
According to the question, we have $ d = d $ , and $ D = b $ . Putting these we get
 $ x = \dfrac{{yd}}{b} $
Finally substituting from (1) we get
 $ x = \dfrac{{\left( {d/2} \right)d}}{b} $
 $ \Rightarrow x = \dfrac{{{d^2}}}{{2b}} $
Thus we get the path difference for the given double slit experimental setup equal to $ \dfrac{{{d^2}}}{{2b}} $ .
Hence, the correct answer is option B.

Note
If we do not remember the formula which is used in the above solution to calculate the path difference, then also we can very easily obtain the answer. We just need to have the figure corresponding to the situation given the question from the figure. Then, we have to consider the geometry of that figure to determine the required expression as $ x = {S_2}P - {S_1}P $ .