Question

The dimension of a metal block is given in the diagram

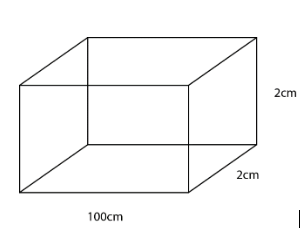
The ratio of $100cm \times 2cm \times 2cm$ resistance between square faces and rectangular faces is
(A) $1:1$
(B) \[25:1\]
(C) $2500:1$
(D) $50:1$

Answer 1

Hint : Use the formula of resistance of the conductor to find the resistance of the square face and the rectangle face. The dimensions of the block is given from that we can know the side of the square and the length and breadth of the rectangle with that find the area of the square and rectangle and substitute those values in the resistance formula then find the ratio of resistance between square faces and rectangular faces.

Complete step by step answer
Resistance offered to a conductor is known as resistivity. The resistivity is defined as the capability of restriction of flow of current.
The resistance of a conductor is directly proportional to the length of the conductor and is inversely proportional to its area of cross section A.
$ \Rightarrow R \propto \dfrac{l}{A}$
$ \Rightarrow R = \dfrac{{\rho l}}{A}$
$\rho $ is the specific resistance or electrical resistivity of the conductor.
l is the length of the conductor
A is the area of the conductor
We have to find the ratio of resistance between square faces and rectangular faces.
Firstly let us calculate the resistance of the square face
The length of the side of the square, $a = 2cm$
The area of the square is $4a$
$ \Rightarrow {\text{A }} = {\text{ 4a}}$
$ \Rightarrow {\text{A }} = {\text{ }}4 \times 2$
$ \Rightarrow {\text{A }} = {\text{ 8cm}}$
We know that the resistance of a conductor is
$ \Rightarrow R = \dfrac{{\rho l}}{A}$
$ \Rightarrow {R_s} = \dfrac{{\rho 2}}{8}$
$ \Rightarrow {R_s} = \dfrac{\rho }{4}{\text{ }} \to {\text{1}}$
Now let us calculate the resistance of the rectangular face
The length of the rectangle, $b = 100cm$
The breadth of the rectangle, $l = 2cm$
The area of the rectangle is $l \times b$
$ \Rightarrow {\text{A }} = {\text{ l}} \times {\text{b}}$
$ \Rightarrow {\text{A }} = {\text{ 2}} \times {\text{100}}$
$ \Rightarrow {\text{A }} = {\text{ 200}}$
We know that the resistance of a conductor is
$ \Rightarrow R = \dfrac{{\rho l}}{A}$
$ \Rightarrow {R_R} = \dfrac{{\rho 2}}{{200}}$
$ \Rightarrow {R_R} = \dfrac{\rho }{{100}}{\text{ }} \to {\text{2}}$
To find the ratio of resistance between square faces and rectangular faces divide the resistance of square faces by rectangular faces
$ \Rightarrow \dfrac{{{R_s}}}{{{R_R}}} = \dfrac{{\dfrac{\rho }{4}}}{{\dfrac{\rho }{{100}}}}$
$ \Rightarrow \dfrac{{{R_s}}}{{{R_R}}} = \dfrac{\rho }{4} \times \dfrac{{100}}{\rho }$
$ \Rightarrow \dfrac{{{R_s}}}{{{R_R}}} = \dfrac{{25}}{1}$
$ \Rightarrow {R_s}:{R_R} = 25:1$
The ratio of resistance between square faces and rectangular faces is $25:1$
Hence the correct answer is option (B) $25:1$.

Note
It is a direct question if we know the basic math formulas and the resistance formula we can easily solve this problem. Most of the students mistook the breadth of the rectangle as the length of the rectangle and put wrong values in the resistance formula, so be careful while substituting the values.