Question

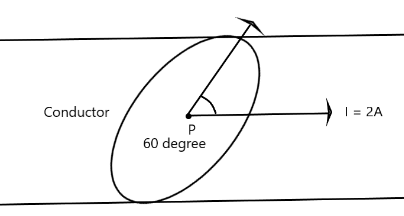
The cross-sectional area of the plane shown in the figure is equal to \[1\,c{{m}^{2}}\].\[2\,A\] current flows through the conductor. The current density at point \[p\] in the conductor will be ?

Answer 1

Hint:The amount of electric current flowing per unit cross-sectional area of a material is termed as current density. Mathematically we can write is current density as\[J=I/(A\cos \theta )\] here \[I\]is current flowing in the conductor, \[A\] is the area of cross section and \[\theta \] is the angle between current direction and area vector. Visualize the situation to get a better idea and use the mentioned formula to get the answer.

Complete step by step answer:
Current density is the amount of electric current flowing per unit cross sectional area of a material, we can write it mathematically as \[J=I/(A\cos \theta )\]. Generally, we write the mentioned formula as current equal to the dot product of current density and area of cross section from where \[\theta \] comes into play.

Before solving the question, keep in mind here, we are considering area as a vector whose direction is perpendicular to the surface or material (in this case conductor). Now
\[A=1\,c{{m}^{2}}={{10}^{(-4)}}\,{{m}^{2}} \\
\Rightarrow I=2A \\
\Rightarrow \theta ={{30}^{\circ }} \\
\Rightarrow \cos \theta =\sqrt{3}/2 \\ \]
Now we know \[J=I/(A\cos \theta )\] putting the values given above we get
\[\therefore J=(4/\sqrt{3})\times {{10}^{4}}\,A/{{m}^{2}}\]

Hence the current density at point \[p\] in the conductor is $(4/\sqrt{3})\times {{10}^{4}}\,A/{{m}^{2}}$.

Note:Such types of questions are normal formula based questions, so one should keep all the formulas in mind. Also there is an interesting thing on which questions are asked, current density is directly proportional to electric field \[J=\sigma E\] where \[\sigma \] is conductivity.