Question

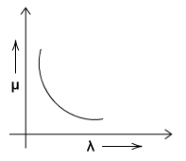
The correct curve between refractive index and wavelength will be
(A)

(B)

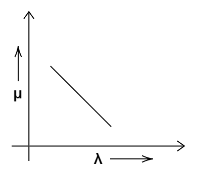
(C)

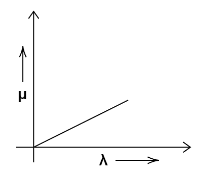
(D)

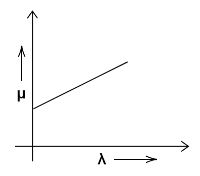
Answer 1

Hint: When the light enters a medium other than the vacuum, it slows down according to the optical density of the medium. Thus the wavelength of the light changes when it travels from medium to medium. Before looking at the graphs, find the mathematical relation between $ \mu $ and $ \lambda $ . Find the meaning of the refractive index and its formula.

Formula used:
 $\Rightarrow v = \lambda f $
 $\Rightarrow \mu = \dfrac{c}{v} $

Complete step by step solution
The speed of light is not the same in different mediums. If a ray of light transmits from one medium to another, the speed of light changes. The medium in which the speed of light is faster is called the rarer medium and the medium in which the speed of light is slower is called the denser medium. When the speed of light changes, it also changes its direction and the light appears to be bending at the interface of the mediums. This bending of light is called refraction. To recognize the speed of light in a medium, we have something known as a refractive index. The Refractive index $ \left( \mu \right) $ of a medium is that characteristic which decides the speed of light.
It is defined as the ratio of the speed of light in vacuum $ (c) $ to the speed of light $ \left( v \right) $ in the given medium i.e $ \mu = \dfrac{c}{v} $ ....... $ \left( 1 \right) $ .
Since light is a wave, it has a frequency and a wavelength. The speed of a wave $ \left( v \right) $ is equal to the product of frequency $ \left( f \right) $ and wavelength $ \left( \lambda \right) $ of the wave i.e
 $ v = \lambda f $ ........ $ \left( 2 \right) $
Substitute the value of $ v $ in equation $ \left( 1 \right) $
Therefore, $ \mu = \dfrac{c}{{f\lambda }} $ ........... $ \left( 3 \right) $
When a wave light travels through different mediums, the frequency of the wave doesn’t change. Therefore, according to the equation $ \left( 2 \right) $ if the speed $ \left( v \right) $ of light changes then wavelength must change.
Consider the equation $ \left( 3 \right) $ . Since $ c $ and $ f $ are constants $ \dfrac{c}{f} $ will also be a constant. Let $ \dfrac{c}{f} = k $ .
Therefore, we can write the equation $ \left( 3 \right) $ as $ \mu = \dfrac{k}{\lambda } \Rightarrow \mu \lambda = k $ .
Since $ k $ is a constant, the product of $ \mu $ and $ \lambda $ will always be constant.
Take certain values of $ \mu $ and $ \lambda $ . If we increase the value of $ \lambda $ then the value $ \mu $ decreases because the product should be constant. From here as we go on increasing the value of $ \lambda $ .
The value $ \mu $ will go on decreasing.
If we check the graphs, the best-suited graph for the above question is (A).

Note
Let us discuss why other graphs show incorrect relation between $ \mu $ and $ \lambda $ . Before going through the other three options. Let’s remember the correct relation. As we continuously increase the value $ \lambda $ , the value $ \mu $ decreases. This relation is all over the graph and it does not change.