Question

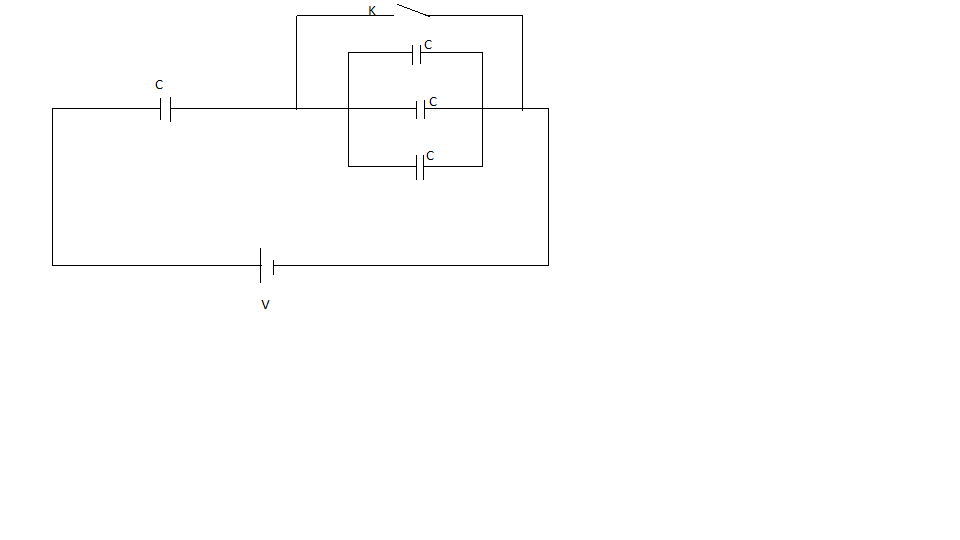
The charge that flows through the cell on closing the key K as shown in the circuit is

$
  1)\;\dfrac{4}{3}CV \\
  2){\text{ }}\dfrac{3}{4}CV \\
  {\text{3) }}\dfrac{{CV}}{4} \\
  4){\text{ 4CV}} \\
 $

Answer 1

Hint: Capacitors are an electronic component which stores energy with the charge and potential difference across the terminals. When one capacitor is attached back to back with others they are said to be in series, whereas when both the terminals of the capacitor are attached with both the terminals of the other capacitor, they are said to be in parallel capacitors.

Complete step by step answer:
Consider the given circuit diagram in two parts.
The capacitor C is in series with the equivalent of the three capacitors.

First we find the Capacitance of the three capacitors connected in parallel and then will find the series connection with the fourth capacitor.

Now, according to the formula, the capacitance of the three capacitors connected in parallel is –
\[
  {C_{eq1}} = C + C + C \\
  {C_{eq1}} = 3C \\
 \]
Now, this capacitance is in series connection –
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{C} + \dfrac{1}{{3C}}$
Do cross-multiplication and find the value of the equivalent capacitance
$
  \dfrac{1}{{{C_{eq}}}} = \dfrac{3}{{3C}} + \dfrac{1}{{3C}} \\
  \dfrac{1}{{{C_{eq}}}} = \dfrac{4}{{3C}} \\
  {C_{eq}} = \dfrac{{3C}}{4}{\text{ }}......{\text{(a)}} \\
 $
Now, after closing the key k, the equivalent Capacitance be $C{'_{eq}} = C$
Therefore, the charge flow \[q' = C{'_{eq\partial }}V = CV\;{\text{ }}......{\text{(b)}}\]
Now, the net charge flow is$ = q' - q$
Place values in the above left hand side of the equation from the equations (a) and (b)

Net charge is
$
   = CV - \dfrac{3}{4}CV \\
   = \dfrac{{4CV - 3CV}}{4} \\
   = \dfrac{{CV}}{4} \\
 $
Hence, from the given options- the option third is the correct answer.

Additional Information: The charge flows from the positive terminal of the battery and goes back to the negative terminal of the battery.

Note:Always remember and apply the correct formula when capacitors connected in series and parallel. Due its simplification carefully and it goes well.