Question

The cells are joined in parallel to get the maximum current when
A. External resistance is very large as compared to the total internal resistance
B. Internal resistance is very large as compared to the external resistance
C. Internal resistance and external resistance are equal
D. Emf of each cell is very large

Answer 1

Hint:The voltage drop across a cell is the difference between the emf of the cell and the voltage across its internal resistance. Use this property to find the current through the circuit to come to a conclusion.

Formula used:
The mathematical expression of the Ohm’s law is given by,
\[V = IR\]
where, \[V\] is the potential difference of the circuit element,\[R\] is the resistance of the circuit element and \[I\] is the current through it.
The equivalent resistance in a parallel circuit is given by,
\[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ....\]
where, \[{R_{eq}}\] is the equivalent resistance of the circuit and \[{R_1}\] ,\[{R_2}\]… are the resistances connected in parallel.

Complete step by step answer:
We have given here two cells that are connected in parallel. Now, if we connect two cells in parallel the net emf due to the cells will be the same as the emf due to one cell in the circuit.So, let the emf of each cell is \[E\].

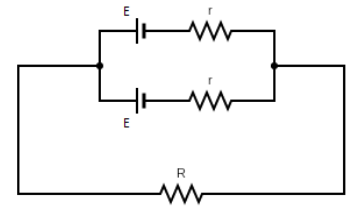
Now, the internal resistance of the cell is the parallel combination of the resistances hence net internal resistance of the battery will be, \[{R_{eq}} = \dfrac{r}{n}\]. Now, let the battery be connected to an external resistance of \[R\]. So, the current through the circuit will be,
\[I = \dfrac{E}{{R + \dfrac{r}{n}}}\]
\[\Rightarrow I = \dfrac{{nE}}{{nR + r}}\]

Now, if the emf of the cells are constant the current to be maximum the term in the denominator must be minimum. This value depends on the value of internal and external resistance of the circuit.
Now if, \[R < < \dfrac{r}{n}\] current in the circuit will be, \[I = \dfrac{{nE}}{r}\].
And if, \[R > > \dfrac{r}{n}\] current in the circuit will be, \[I = \dfrac{E}{R}\].
So, we can see that the current will be maximum if the internal resistance of the circuit is very large than the external resistance of the circuit. Since, the current is a factor of the number of cells added in parallel. So, the maximum current is when the internal resistance is very large as compared to the external resistance

Hence, option B is the correct answer.

Note:The current will be more if the number of cells are more. If the cells are connected in series the resistance in the circuit will simply add up then the net current in the circuit will be, \[I = \dfrac{{nE}}{{R + nr}}\]. In this case if the external resistance is very large then the current in the circuit will be maximum.