Question

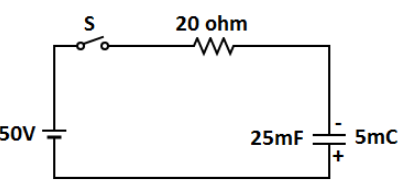
The capacitor $C$ is charged to $5\,mC$ when the switch $S$ in the circuit given below is kept open. If at $t = 0\sec $ switch $S$ is closed, the variation of potential drop ${V_R}$ across the resistance $20\Omega $ with time is represented by:

Answer 1

Hint: In the given circuit, the capacitor will get charged with time and firstly we will find the charge on the capacitor at a particular time and then we will find the charging and discharging current which is time derivative of charge variable.

Complete step by step answer:
Let us convert the initial charge of capacitor into coulomb.$5mc = 5 \times {10^{ - 3}}C$ And let $q(t)$ be the charge varies with time and value of $\dfrac{1}{{RC}} = 2000\sec $
$q(t) = \dfrac{1}{{200}}{e^{ - 2000t}}$
Now we also know that,
Discharging current can be written as $i(t) = \dfrac{{dq(t)}}{{dt}}$
$i(t) = - 10{e^{ - 2000t}} \to (i)$
Since, for charging the capacitor, the current with time is written as
$\dfrac{{dq}}{{q - VC}} = - \dfrac{1}{{RC}}dt$
$\Rightarrow \ln (q - VC) = - \dfrac{1}{{RC}}t + \ln K$
Since at time equals to zero this charge $q = 0$ hence,
$q(t) = 1.25 \times {10^{ - 3}}(1 - {e^{ - 2000t}})$
differentiating above equation with respect to time, we will get the current as:
$i(t) = 6.25 \times {10^{ - 3}} \times 2 \times {e^{ - 2000t}}$
$\Rightarrow i(t) = 12.50\,{e^{ - 2000t}}A$
$\therefore {V_R}(t) = 250\,{e^{ - 2000t}}V$
Now, we have the value of voltage and the current. Now, we can draw a graph between voltage versus time keeping voltage in Y-direction and time on X-direction. So the graph can be represented as:

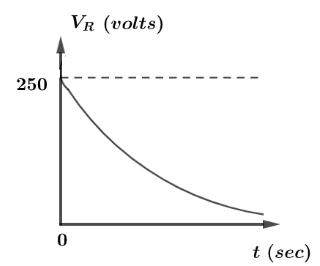
Hence, above is the variation between voltages across the resistor with time.

Note:It should be remembered that, the negative of Euler constant with a negative exponent is a decreasing graph with dependent variable while Euler constant having a positive exponent has an increasing graph with dependent variable and hence, in this case Euler constant has a negative slope.