Question

The area (in sq.units) of the part of the circle \[{{x}^{2}}+{{y}^{2}}=36\], which is outside the parabola ${{y}^{2}}=9x$, is:
a) $24\pi +3\sqrt{3}$
b) $12\pi +3\sqrt{3}$
c) $12\pi -3\sqrt{3}$
d) $24\pi -3\sqrt{3}$

Answer 1

Hint:
For the question, we are provided with equation of circle which is \[{{x}^{2}}+{{y}^{2}}=36\] and also the equation for the parabola ${{y}^{2}}=9x$. We need to evaluate the area of the part of the circle that lies outside parabola. We calculate the area of the circle and subtract the area of the parabola lying in the circle.

Complete step by step solution:
For better understanding, let us create the figure for given question;
We know standard equation for circle \[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\]
Comparing with given equation \[{{x}^{2}}+{{y}^{2}}=36\]; we get r = 6units
Solving \[{{x}^{2}}+{{y}^{2}}=36\] and ${{y}^{2}}=9x$ simultaneously;
${{x}^{2}}+9x-36=0$
Solving above quadratic equation
${{x}^{2}}-3x+12x-36=0$
$x\left( x-3 \right)+12\left( x-3 \right)=0$
$\left( x-3 \right)\left( x+12 \right)=0$
$\left( x-3 \right)=0$ Or $\left( x+12 \right)=0$
The above equations give value for x as \[x=3, -12\]
x cannot be negative as it will not satisfy the given equation for parabola
Thus, we have x=3

Figure:

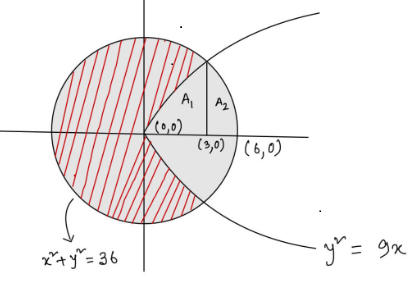
Area of circle = \[\pi r^{2}\]
Now, Required area(A) can be calculated by deducting the area of the parabola inside the circle from the area of the circle. It can be given as;
$A=\pi {{r}^{2}}-2\left[ A_1+A_2 \right]$
\[A=\pi {{6}^{2}}-2\left[ \left( \int\limits_{0}^{3}{\sqrt{9x}dx} \right)+\left( \int\limits_{3}^{6}{\sqrt{36-{{x}^{2}}}dx} \right) \right]\]

\[A=36\pi -2\left[ \left[ 3\times \frac{2}{3}{{x}^{\frac{3}{2}}} \right]_{0}^{3}+\left[ \frac{x}{2}\sqrt{{{36}^{2}}-{{x}^{2}}}+\frac{36}{2}{{\sin }^{-1}}\frac{x}{6} \right]_{3}^{6} \right]\]

\[A=36\pi -2\left[ \left[ 6\sqrt{3}-0 \right]+\left[ \left( 0+18{{\sin }^{-1}}\frac{6}{6} \right)-\left( \frac{3}{2}\times 3\sqrt{3}+18{{\sin }^{-1}}\frac{3}{6} \right) \right] \right]\]
\[A=36\pi -2\left[ \left[ 6\sqrt{3} \right]+\left[ \left( \frac{3}{2}\times 3\sqrt{3}+\frac{18\pi }{6} \right) \right] \right]\]
Simplifying further we get,
\[A=36\pi -\left( 12\sqrt{3}+18\pi -9\sqrt{3}-6\pi \right)\]
Opening brackets to simplify
\[A=24\pi -3\sqrt{3}\]

Thus we get area of circle outside the given parabola as \[A=24\pi -3\sqrt{3}\]

Correct Option: (d) $24\pi -3\sqrt{3}$

Note: It is mandatory to understand the given equations. Plotting a diagram would help better understanding. Such types of questions could be solved with basic knowledge of curves and finding areas using integration. Following mentioned are some of the important formulas to remember.

$1.\int{\sqrt{{{x}^{2}}+{{a}^{2}}}}dx=\frac{1}{2}\left[ x\sqrt{{{x}^{2}}+{{a}^{2}}}+{{a}^{2}}\log \left( \left| x+\sqrt{{{x}^{2}}+{{a}^{2}}} \right| \right) \right]+C$
$2.\int{\sqrt{{{a}^{2}}-{{x}^{2}}}}dx=\frac{1}{2}\left[ x\sqrt{{{a}^{2}}-{{x}^{2}}}+{{a}^{2}}{{\sin }^{-1}}\left( \frac{x}{a} \right) \right]+C$
$3.\int{\sqrt{{{x}^{2}}-{{a}^{2}}}}dx=\frac{1}{2}\left[ x\sqrt{{{x}^{2}}-{{a}^{2}}}-{{a}^{2}}\log \left( \left| x+\sqrt{{{x}^{2}}-{{a}^{2}}} \right| \right) \right]+C$