
The area enclosed between the curves \[y = lo{g_e}(x + e)\], \[x = lo{g_e}\left( {\dfrac{1}{y}} \right)\;\] and the x-axis is
A) $2$ sq. units
B) $1$ sq. units
C) $4$ sq. units
D) None of these
Answer
232.8k+ views
Hint: In this we are given the equation of two curves. Firstly, convert the second curve in the form of $x$ because we need to find the area till $x - axis$. Now, using the first curve calculate the coordinate on $x - axis$ by taking $y = 0$. Calculate the area by the integration of the required equation of the curve and solve it further by applying the ILATE rule.
Formula Used: ILATE Rule of integration
Here, the full form of ILATE is Inverse, Logarithms, Algebraic, Trigonometric, and Exponential. We use this series to select which of the first will be $\left( {u\left( x \right)} \right)$ or $\left( {v\left( x \right)} \right)$. Here, the first function will be the function that comes first in this series.
$\int {u(x)v\left( x \right)dx = u\left( x \right)\int {v\left( x \right)dx} - \int {\left( {\dfrac{{du\left( x \right)}}{{dx}}\int {v\left( x \right)dx} } \right)} dx} $
Lorartithm formula –
$\log 1 = 0$
$\log e = 0.43429$
${a^x} = y \Leftrightarrow {\log _a}y = x$
Complete step by step Solution:
We are given two equations of curve \[y = lo{g_e}(x + e)\] and \[x = lo{g_e}\left( {\dfrac{1}{y}} \right)\;\]
We have \[x = lo{g_e}\left( {\dfrac{1}{y}} \right)\;\]
Also written as,
$x = {\log _e}1 - {\log _e}y$
$x = - {\log _e}y$
${\log _a}y = - x$
$y = {e^{ - x}}$
For \[y = lo{g_e}(x + e)\], we’ll shift the graph of the curve $y = {\log _e}x$, $e$ units at the left-hand side because at $y = 0$ the value of $x = 1 - e$
Let’s mark all the curves in the graph, Graph is attached below;
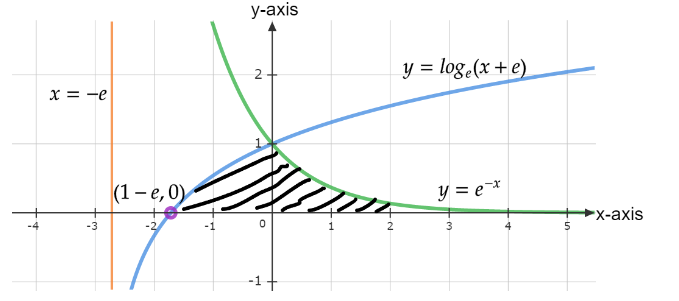
Figure 1: A Graph of given curves with the point (1-e,0)
Now, the area of the shaded region will be
$A = \int\limits_{1 - e}^0 {1 \times {{\log }_e}\left( {x + e} \right)dx} + \int\limits_0^\infty {{e^{ - x}}dx} $
Applying ILATE rule, i.e., $\int {u(x)v\left( x \right)dx = u\left( x \right)\int {v\left( x \right)dx} - \int {\left( {\dfrac{{du\left( x \right)}}{{dx}}\int {v\left( x \right)dx} } \right)} dx} $
$ = \left[ {x{{\log }_e}\left( {x + e} \right)} \right]_{1 - e}^0 - \int\limits_{1 - e}^0 {\dfrac{x}{{x + e}}dx} - \left[ {{e^{ - x}}} \right]_0^\infty $
$ = \left[ {\left( 0 \right){{\log }_e}\left( {0 + e} \right) - \left( {1 - e} \right){{\log }_e}\left( {1 - e + e} \right)} \right] - \int\limits_{1 - e}^0 {\dfrac{{x + e - e}}{{x + e}}dx} - \left( {{e^{ - \infty }} - {e^0}} \right)$
As we know, $\log 1 = 0$
$ = 0 - \int\limits_{1 - e}^0 {1 - \dfrac{e}{{x + e}}dx} - \left( {0 - 1} \right)$
$ = - \left[ {x - e\log \left( {x + e} \right)} \right]_{1 - e}^0 + 1$
$ = - \left[ {0 - e\log \left( {0 + e} \right) - \left( {1 - e} \right) + e\log \left( {1 - e + e} \right)} \right] + 1$
$ = - \left[ { - e - 1 + e + e\left( 0 \right)} \right] + 1$
$ = 2$ sq. Units
Therefore, the correct option is (A).
Note: To solve such a question, one should have a good knowledge of logarithm and integration formulas. Also, if you are changing the function and then always change the limits too. Put the limits in the same to calculate new limits. Try to open terms using trigonometric identities as much as it is possible. And to solve the limits, firstly solve the integration past then last subtract the terms (put the upper limit values and then lower limits).
Formula Used: ILATE Rule of integration
Here, the full form of ILATE is Inverse, Logarithms, Algebraic, Trigonometric, and Exponential. We use this series to select which of the first will be $\left( {u\left( x \right)} \right)$ or $\left( {v\left( x \right)} \right)$. Here, the first function will be the function that comes first in this series.
$\int {u(x)v\left( x \right)dx = u\left( x \right)\int {v\left( x \right)dx} - \int {\left( {\dfrac{{du\left( x \right)}}{{dx}}\int {v\left( x \right)dx} } \right)} dx} $
Lorartithm formula –
$\log 1 = 0$
$\log e = 0.43429$
${a^x} = y \Leftrightarrow {\log _a}y = x$
Complete step by step Solution:
We are given two equations of curve \[y = lo{g_e}(x + e)\] and \[x = lo{g_e}\left( {\dfrac{1}{y}} \right)\;\]
We have \[x = lo{g_e}\left( {\dfrac{1}{y}} \right)\;\]
Also written as,
$x = {\log _e}1 - {\log _e}y$
$x = - {\log _e}y$
${\log _a}y = - x$
$y = {e^{ - x}}$
For \[y = lo{g_e}(x + e)\], we’ll shift the graph of the curve $y = {\log _e}x$, $e$ units at the left-hand side because at $y = 0$ the value of $x = 1 - e$
Let’s mark all the curves in the graph, Graph is attached below;

Figure 1: A Graph of given curves with the point (1-e,0)
Now, the area of the shaded region will be
$A = \int\limits_{1 - e}^0 {1 \times {{\log }_e}\left( {x + e} \right)dx} + \int\limits_0^\infty {{e^{ - x}}dx} $
Applying ILATE rule, i.e., $\int {u(x)v\left( x \right)dx = u\left( x \right)\int {v\left( x \right)dx} - \int {\left( {\dfrac{{du\left( x \right)}}{{dx}}\int {v\left( x \right)dx} } \right)} dx} $
$ = \left[ {x{{\log }_e}\left( {x + e} \right)} \right]_{1 - e}^0 - \int\limits_{1 - e}^0 {\dfrac{x}{{x + e}}dx} - \left[ {{e^{ - x}}} \right]_0^\infty $
$ = \left[ {\left( 0 \right){{\log }_e}\left( {0 + e} \right) - \left( {1 - e} \right){{\log }_e}\left( {1 - e + e} \right)} \right] - \int\limits_{1 - e}^0 {\dfrac{{x + e - e}}{{x + e}}dx} - \left( {{e^{ - \infty }} - {e^0}} \right)$
As we know, $\log 1 = 0$
$ = 0 - \int\limits_{1 - e}^0 {1 - \dfrac{e}{{x + e}}dx} - \left( {0 - 1} \right)$
$ = - \left[ {x - e\log \left( {x + e} \right)} \right]_{1 - e}^0 + 1$
$ = - \left[ {0 - e\log \left( {0 + e} \right) - \left( {1 - e} \right) + e\log \left( {1 - e + e} \right)} \right] + 1$
$ = - \left[ { - e - 1 + e + e\left( 0 \right)} \right] + 1$
$ = 2$ sq. Units
Therefore, the correct option is (A).
Note: To solve such a question, one should have a good knowledge of logarithm and integration formulas. Also, if you are changing the function and then always change the limits too. Put the limits in the same to calculate new limits. Try to open terms using trigonometric identities as much as it is possible. And to solve the limits, firstly solve the integration past then last subtract the terms (put the upper limit values and then lower limits).
Recently Updated Pages
JEE Main 2026 Session 2 Registration Open, Exam Dates, Syllabus & Eligibility

JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding Average and RMS Value in Electrical Circuits

Understanding Collisions: Types and Examples for Students

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Understanding Atomic Structure for Beginners

JEE Main Syllabus 2026: Download Detailed Subject-wise PDF

Other Pages
JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Inductive Effect and Its Role in Acidic Strength

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Chemistry Question Papers for JEE Main, NEET & Boards (PDFs)

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Keys & Solutions

If y xxx cdots infty then find dfracdydx A yxy 1 B class 12 maths JEE_Main




