Question

The area bounded by the parabola $ {{\text{x}}^{2}} $ = 4ay, x – axis and the straight line y =2a is:
(a) 16 $ \sqrt{2}{{a}^{2}} $ sq. units
(b) $ \dfrac{16\sqrt{2}}{3}{{a}^{2}} $ sq. units
(c) $ \dfrac{32\sqrt{2}}{3}{{a}^{2}} $ sq. units
(d) $ \dfrac{32\sqrt{2}}{5}{{a}^{2}} $ sq. units

Answer 1

Hint: We will first draw a figure to understand the question better. Then we will find the points at which the straight line and the parabola intersects. To find the points, we have to solve the given solutions Once we find the points, we will find the area under the straight line and the curve between the two intersecting points. Then we will find the difference between the total areas under the curves to find the area between the curves.

Complete step-by-step answer:
The diagram of the curves will be as follows:
 

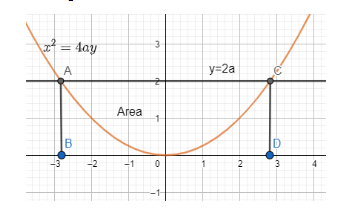
Thus, we can see that the parabola $ {{\text{x}}^{2}} $ = 4ay lies below the line y = 2a.
As we can see, to find the area between the curves, we need to find the area under the line y = 2a until the x – axis and between the points of intersection of parabola $ {{\text{x}}^{2}} $ = 4ay and line y = 2a. Then we will find the area under the parabola until the x – axis and subtract it from the area under y = 2a. The result will be the area between parabola $ {{\text{x}}^{2}} $ = 4ay and line y = 2a.
To find the points of intersections, we will solve the equation of parabola $ {{\text{x}}^{2}} $ = 4ay and line y = 2a.
To solve, we will substitute y = 2a in the equation $ {{\text{x}}^{2}} $ = 4ay.
 $ \begin{align}
  & \Rightarrow {{x}^{2}}=4a\left( 2a \right) \\
 & \Rightarrow {{x}^{2}}=8{{a}^{2}} \\
 & \Rightarrow x=\pm 2\sqrt{2}a \\
\end{align} $
Thus, the two points at which the line and the parabola intersects are $ \left( -2\sqrt{2}a,2a \right) $ and $ \left( 2\sqrt{2}a,2a \right) $ .
From the figure, the space between the x – axis and y = 2a is rectangular. The breadth of this rectangle will be equal to 2a and the length will be the distance between the two points of intersection.
The distance between the points of intersection is $ 4\sqrt{2}a $ .
Thus, area under the line y = 2a is $ 4\sqrt{2}a\times 2a $ = $ 8\sqrt{2}{{a}^{2}} $ .
Now, to find the area under the parabola, we will integrate the equation of parabola between the limits $ -2\sqrt{2}a $ and $ 2\sqrt{2}a $ .
Thus, area under parabola = $ \int\limits_{-2\sqrt{2}a}^{2\sqrt{2}a}{\dfrac{{{x}^{2}}}{4a}} $
 $ \Rightarrow $ A = \[\dfrac{2}{4a}\int\limits_{0}^{2\sqrt{2}a}{{{x}^{2}}}\]
 $ \Rightarrow $ A = \[\dfrac{1}{2a}{{\left[ \dfrac{{{x}^{3}}}{3} \right]}_{0}}^{2\sqrt{2}a}\]
 $ \Rightarrow $ A = \[\dfrac{1}{6a}\left( 16\sqrt{2}{{a}^{3}}-0 \right)\]
 $ \Rightarrow $ A = \[\dfrac{8\sqrt{2}{{a}^{2}}}{3}\]
Thus, the area between the x – axis and the parabola is \[\dfrac{8\sqrt{2}{{a}^{2}}}{3}\].
Therefore, the area between the straight line and parabola is given as the difference between the area under the line and the area under the parabola.
 $ \Rightarrow $ A(final) = $ 8\sqrt{2}{{a}^{2}}-\dfrac{8\sqrt{2}{{a}^{2}}}{3} $
 $ \Rightarrow $ A(final) = $ \dfrac{16\sqrt{2}}{3}{{a}^{2}} $
Thus, the area between the line and the curve is $ \dfrac{16\sqrt{2}}{3}{{a}^{2}} $ .
So, the correct answer is “Option B”.

Note: During integration, we used the rule $\int\limits_{-a}^{a}{f\left( x \right)}=2\int\limits_{0}^{a}{f\left( x \right)}$. It is good practice to draw a diagram before solving the question. We can find the area under the line y = 2a with the help of integration also, but it was after drawing the diagram we deduced that the area is rectangular and hence could be found without integration. Thus, drawing diagrams always brings out a clear picture of the problem.