Question

The angle between two diagonals of cube is
A. $30{}^\circ $
B. $45{}^\circ $
C. ${{\cos }^{-1}}\left( \dfrac{1}{3} \right)$
D. ${{\cos }^{-1}}\left( \dfrac{1}{\sqrt{3}} \right)$

Answer 1

Hint: Select a cube and note the diagonals and its points. Select any one pair of diagonals and use the formula of angle between two vectors and solve it. You will get the answer.

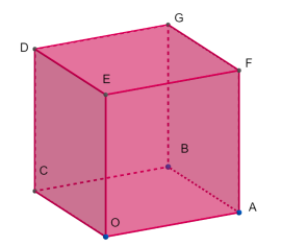
So above we can see the Cube.
So the cube is a symmetrical three-dimensional shape, either solid or hollow, contained by six equal squares. The cube is the only regular hexahedron and is one of the five Platonic solids. It has $6$ faces, $12$ edges, and $8$ vertices.
The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations.
The cube is dual to the octahedron. It has cubical or octahedral symmetry.
The cube is the only convex polyhedron whose faces are all squares.

Cube has its length, breadth and height equal to each other.
Cube It has all its faces in a square shape. In a cube All the faces or sides have equal dimensions.
The plane angles of the cube are the right angle. Each of the faces meets the other four faces.
Each of the vertices meets the three faces and three edges. The edges opposite to each other are parallel.

Let $OABCDEFG$ be a cube with vertices as below,
$O(0,0,0), A(a,0,0), B(a,a,0), C(0,a,0,), D(0,a,a), E(0,0,a), F(a,0,a), G(a,a,a)$

There are four diagonals of the cube: they are $OG,CF,AD$ and $BE$ for the cube.
Let us consider any two say $OG$ and $AD$,
We know that if $A({{x}_{1}},{{y}_{1}},{{z}_{1}})$ and $B({{x}_{2}},{{y}_{2}},{{z}_{2}})$ are two points in space then,
\[\overrightarrow{AB}=({{x}_{2}}-{{x}_{1}})i+({{y}_{2}}-{{y}_{1}})j+({{z}_{2}}-{{z}_{1}})k\]
$\overrightarrow{OG}=(a-0)i+(a-0)j+(a-0)k=ai+aj+ak$
And $\overrightarrow{AD}=(0-a)i+(a-0)j+(a-0)k=-ai+aj+ak$,
So therefore we get the modulus of $\overrightarrow{OG}$ and $\overrightarrow{AD}$,
$\left| \overrightarrow{OG} \right|=\sqrt{{{a}^{2}}+{{a}^{2}}+{{a}^{2}}}=a\sqrt{3}$and$\left| \overrightarrow{AD} \right|=\sqrt{{{(-a)}^{2}}+{{a}^{2}}+{{a}^{2}}}=a\sqrt{3}$
So we know $\overrightarrow{OG}.\overrightarrow{AD}=\left( ai+aj+ak \right).\left( -ai+aj+ak \right)=-{{a}^{2}}\left( i.i \right)+{{a}^{2}}\left( j.j \right)+{{a}^{2}}\left( k.k \right)$

So we know that angle between two vectors $\overrightarrow{a}.\overrightarrow{b}$ is given by,
$\theta ={{\cos }^{-1}}\left( \dfrac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} \right|\overrightarrow{\left| b \right|}} \right)$,
So applying above, so the angle between two diagonals $\overrightarrow{OG}$and$\overrightarrow{AD}$is as follows,
Consider the angle between two diagonals be $\theta $,
So we get the angle as,
$\theta ={{\cos }^{-1}}\left( \dfrac{\overrightarrow{OG}.\overrightarrow{AD}}{\left| \overrightarrow{OG} \right|\left| \overrightarrow{AD} \right|} \right)$
So substituting above values, we get,
$\theta ={{\cos }^{-1}}\left( \dfrac{{{a}^{2}}}{a\sqrt{3}\times a\sqrt{3}} \right)$
So we get,
$\theta ={{\cos }^{-1}}\left( \dfrac{1}{3} \right)$
So the correct answer is option(C).

Note: Be careful about the points$A({{x}_{1}},{{y}_{1}},{{z}_{1}})$and$B({{x}_{2}},{{y}_{2}},{{z}_{2}})$. Sometimes we get confused between the points. So take care of it. The angle between two vectors $\overrightarrow{a}.\overrightarrow{b}$ is $\theta ={{\cos }^{-1}}\left( \dfrac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} \right|\overrightarrow{\left| b \right|}} \right)$. So you should be familiar with the formula. There are four diagonals $OG,CF,AD$ and $BE$. You can consider any one pair of diagonals.