Question

What is the term symbol for Cr in $ {[Cr{(CN)_6}]^{ - 4}} $ ?

Answer 1

Hint: The term symbol in quantum mechanics is an abbreviated description of the angular momentum quantum numbers in a multi-electron system. Every energy level is not only described by its configuration but also its term symbol. The term symbol usually assumes LS coupling.

Complete Step By Step Answer:
The term symbol has a form of: $ ^{2S + 1}{L_J} $
Where $ 2S + 1 $ is the spin multiplicity, L is the orbital quantum number having values S, P, D, F, G, etc. and J is the total angular momentum quantum number. The value of J ranges from $ {J_{\max }} - {J_{\min }} $ (max to min) . The value of $ {J_{\max }} = |L + S| $ and $ {J_{\min }} = |L - S| $
The spin multiplicity or the total spin angular momentum can be given as: $ S = |{M_S}| = |\sum\limits_i {{m_{s,i}}} | $ for I no. of electrons. And total orbital angular momentum quantum number L can be given as: $ L = |{M_L}| = |\sum\limits_i {{m_{l,i}}} | $ for I no. of electrons. If the value of L =0,1,2,3,4, etc. it corresponds to L = S,P,D,F,G, etc, respectively.
 We are given the complex $ {[Cr{(CN)_6}]^{ - 4}} $ . According to the spectrochemical series CN is a strong field ligand and promotes low spin complexes and pairing or electrons instead of exciting them to the higher energy level. The oxidation state of Cr in the complex is +2. The electronic configuration thus becomes:
 $ Cr:[Ar]3{d^4}4{s^2} $
 $ C{r^{ + 2}}:[Ar]3{d^4} $
Therefore, it has four electrons to be arranged in the octahedral crystal field splitting of d orbital. The splitting of d orbital for Octahedral complexes happens as below

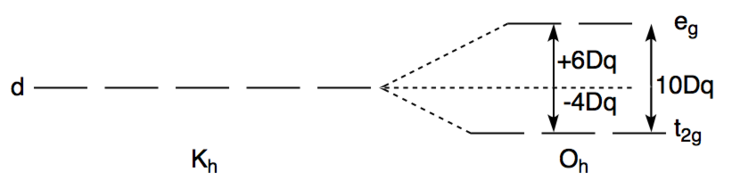
While arranging the 4 electrons in the low field pattern we will get 4 electrons in the lower $ {t_{2g}} $ orbital only. $ {d_{xy}} $ will have 2 electrons, $ {d_{xz}},{d_{yz}} $ will have one electron each.

Now, since we know the electronic configuration let us find the term symbols.
The total spin angular momentum can be given as: $ S = |{M_S}| = |\sum\limits_i {{m_{s,i}}} | $
For the given configuration of electrons the value of $ S = \dfrac{1}{2} - \dfrac{1}{2} + \dfrac{1}{2} + \dfrac{1}{2} = 1 $
The spin multiplicity will be equal to $ {S_m} = 2S + 1 = 2(1) + 1 = 3 $ . Spin multiplicity = 3 indicates Triplet state.
The value of total orbital angular momentum quantum number L can be given as: $ L = |{M_L}| = |\sum\limits_i {{m_{l,i}}} | $
The doubly occupied orbital will have a $ {m_l} = - 2 $ and singly occupied orbitals will have $ {m_l} = - 1,0 $ respectively. The total angular momentum quantum number L will be: $ L = | - 2 - 1 + 0| = | - 5| = 5 \to H $
The term symbol until now can be written as $ ^3H $
The value of J will be from $ {J_{\max }} = |L + S| $ to $ {J_{\min }} = |L - S| $ i.e. from $ {J_{\min }} = |5 - 1| = 4 $ to $ {J_{\max }} = |5 + 1| = 6 $ . Therefore, the value of J will be $ J = 4,5,6 $
Substituting the values to find the term symbols for $ {[Cr{(CN)_6}]^{ - 4}} $ : $ ^3{H_4}{,^3}{H_5}{,^3}{H_6} $
This is the required answer.

Note:
If we are asked the ground state term symbol, the value of J will be $ {J_{\min }} = |L - S| $ for less than half filled orbitals and $ {J_{\max }} = |L + S| $ for more than half filled orbitals. In this case the orbital is less than half filled, hence the value of J will be $ {J_{\min }} = |5 - 1| = 4 $ and the ground state term symbol will be $ ^3{H_4} $ .