Question

How do you tell whether a function is even, odd or neither?

Answer 1

Hint: We are asked about how we can verify that a function is even or odd or neither. To answer this we will learn what even function and odd functions are and then what the criteria are to check which one is even or odd. Then we will look at what functions are neither of them. Then we will work with some examples of each type to get a better understanding of the given type.

Complete step by step solution:
We are asked to find a way to test if a function is even or odd or neither of the two. To do so we will learn what these functions are. First, we will start with an even function.
Even functions are those functions which are symmetric about the y – axis, just like a reflection along the y – axis. For example

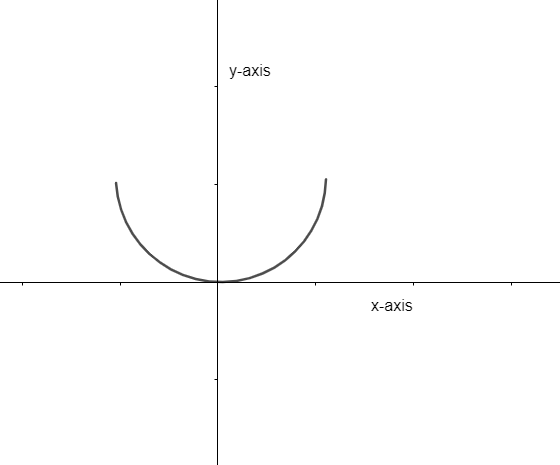
This function is the same along the y – axis. So, this function is an even function. So, one way to check an even function is to make a graph and then look if it is symmetric with the y-axis or not. Also, if a function is even, then it always satisfies that f(x) is the same as f(– x) that is f is even then f(x) = f(– x). So, we can also use this to decide if a function is even or not. For example \[f\left( x \right)={{x}^{2}}\] then
\[f\left( 2 \right)={{2}^{2}}=4\]
\[f\left( -2 \right)={{\left( -2 \right)}^{2}}=4\]
\[f\left( x \right)={{x}^{2}}\]
\[f\left( -x \right)={{\left( -x \right)}^{2}}={{x}^{2}}\]
So, it is an even function.
Now we will work on odd functions. Those functions which are symmetric along the origin are known as an odd function. Consider a graph of f(x) = x.

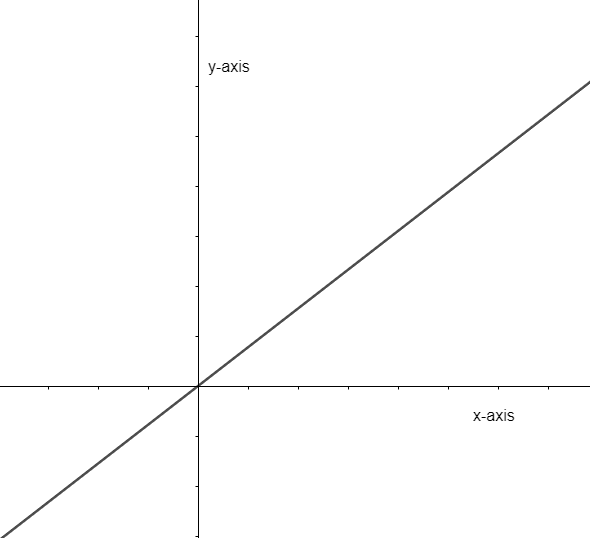
So, this function is the same along with the origin. So, f(x) = x is an odd function. Another way to check the odd function is that the odd function satisfies the property. f(– x) is the same as – f(x). That is, \[f\left( -x \right)=-f\left( x \right).\]
For example,
\[f\left( x \right)=x\]
\[f\left( -x \right)=-x\]
\[\Rightarrow f\left( -x \right)=-\left( x \right)\]
\[\Rightarrow f\left( -x \right)=-f\left( x \right)\]
So, f(x) is an odd function.
If any function does not satisfy f(x) = f (– x) and f(– x) = – f(x) that is the function which is neither odd nor even, that function will come under the category of neither.

Note: In polynomial function, the polynomials with odd power are always odd and polynomials with even power are even. The constant function is always even. Let us consider f(x) = 3 constant function, then f(2) = 3 and f(– 2) = 3. So, f(2) = f(– 2) = 3 always. So, it is even function as it satisfies f(x) = f(– x) = 3.