Question

Study the velocity-time graph of a car is given below and solve the given questions.

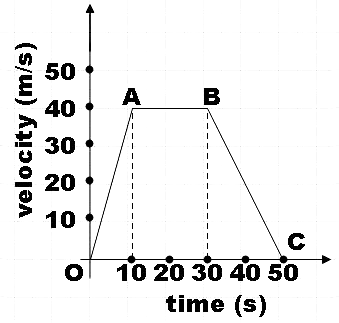
(a) What type of motion is represented by OA?
(b) What type of motion is represented by AB?
(c) What type of motion is represented by BC?
(d) Find the acceleration of the body from O to A.
(e) Find out retardation of the body from B to C.
(f) Find out the distance travelled by the body from A to B.

Answer 1

Hint: You could carefully analyze the given plot thus determine the motion represented by OA, AB and BC. Now you could recall the expression for acceleration and retardation of a body and thus answer the question. Also, recall that the area under the velocity-time graph will give us the distance.

Formula used:
Acceleration,
$a=\dfrac{\Delta v}{\Delta t}$

Complete Step by step solution:
(a) In the given velocity time graph, we see that from point O to point A, the velocity changes uniformly with increase in time. That is, we could say that acceleration is uniform for the motion represented by OA.

So, we found that OA represents uniformly accelerated motion.

(b) From point A to point B, we see that velocity of the body is remaining constant at$40m{{s}^{-1}}$. So the body will have zero acceleration.

So, we could simply say that AB represents uniform motion.

(c) Now from point B to point C, we see that the velocity is changing uniformly with increasing time. But we can also see that the velocity is actually decreasing with the passage of time.

So, the motion represented by BC would be uniform retarded motion.

(d) Acceleration of the body from point O to point A,
$a=\dfrac{\Delta v}{\Delta t}$
$\Rightarrow {{a}_{OA}}=\dfrac{{{v}_{A}}-{{v}_{O}}}{{{t}_{A}}-{{t}_{O}}}$
$\Rightarrow {{a}_{OA}}=\dfrac{40-0}{10-0}$
$\therefore {{a}_{OA}}=4m{{s}^{-2}}$

The acceleration is found to be $4m{{s}^{-2}}$ for OA.

(e) Retardation of the body from point B to point C.
$a=\dfrac{\Delta v}{\Delta t}$
$\Rightarrow {{a}_{BC}}=\dfrac{{{v}_{C}}-{{v}_{B}}}{{{t}_{C}}-{{t}_{B}}}$
$\Rightarrow {{a}_{BC}}=\dfrac{0-40}{50-30}$
$\therefore {{a}_{BC}}=-2m{{s}^{-2}}$

The deceleration is found to be $-2m{{s}^{-2}}$ for BC.

(f) Here, we are asked to find the distance travelled by the body from point A to point B.
You may recall that the area under the velocity-time graph will give us the distance travelled. So, the area under AB is found to be a rectangle whose area is given by,
$Area=l\times b$
Where, l = length = 40
b = breadth = 30-10 = 20
$\Rightarrow A=l\times b$
$\therefore A=40\times 20=800m$

Therefore, we found that the distance covered by the body from point A to B is 800m.

Note:
You may have noted that we have used the same expression for finding the acceleration as well as the retardation of the body. You shouldn’t assume that the acceleration and retardation are two different concepts. Acceleration is when the velocity is increasing with time and retardation happens when the velocity decreases with time, but both are time rate of change of velocity.