
Solve graphically the system of equations
$4x-3y+4=0$
$4x+3y-20=0$
Find the area bounded by these lines and x-axis.
Answer
604.5k+ views
Hint: A line can be completely determined by two points. So, to draw the line just take two points which satisfy the line equation and draw a line through those points in the graph. Plot these lines on the same graph and find the coordinates of their point of intersection. This will give the solution of the given system of equations.
Complete step-by-step answer:
For equation $4x-3y+4=0$
When x = 0 we have $4\times 0-3y+4=0$
$\begin{align}
& \Rightarrow -3y+4=0 \\
& \Rightarrow -3y=0-4 \\
& \Rightarrow -3y=-4 \\
& \Rightarrow y=\dfrac{-4}{-3} \\
\end{align}$
i.e. $y=\dfrac{4}{3}$
When y = 0 we have $4x-3\times 0+4=0$
$\begin{align}
& \Rightarrow 4x-0+4=0 \\
& \Rightarrow 4x+4=0 \\
& \Rightarrow 4x=-4 \\
& \Rightarrow x=\dfrac{-4}{4} \\
\end{align}$
i.e. $x=-1$
We plot the points A $\left( 0,\dfrac{4}{3} \right)$ and B$\left( -1,0 \right)$ and draw a line through the points.

So, we have AB $\equiv 4x-3y+4=0$
For equation $4x+3y-20=0$
When x = 0, $4\times 0+3y-20=0$
$\begin{align}
& \Rightarrow 0+3y-20=0 \\
& \Rightarrow 3y-20=0 \\
& \Rightarrow 3y=20 \\
& \Rightarrow y=\dfrac{20}{3} \\
\end{align}$
i.e. $y=\dfrac{20}{3}$
When y = 0, we have $4x+3\times 0-20=0$
$\begin{align}
& \Rightarrow 4x+0-20=0 \\
& \Rightarrow 4x=20 \\
& \Rightarrow 4x=20 \\
& \Rightarrow x=\dfrac{20}{4} \\
\end{align}$
i.e. $x=5$
We plot points C $\left( 0,\dfrac{20}{3} \right)$ and D \[\left( 5,0 \right)\] and draw line CD on the same graph.
So, CD $\equiv 4x+3y-20=0$
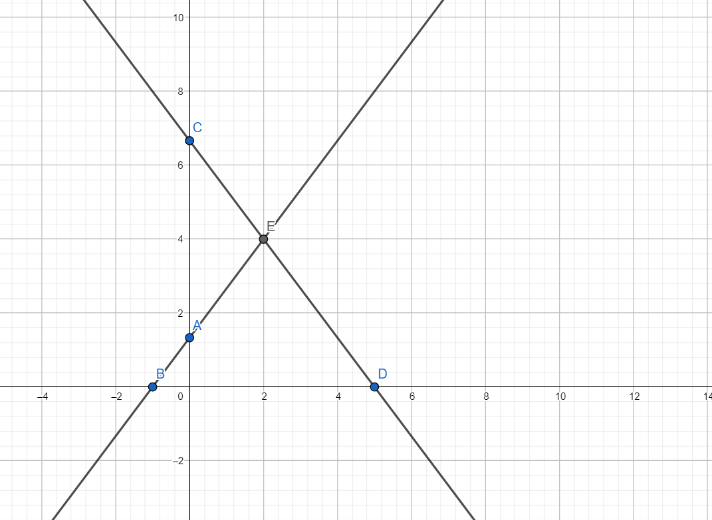
These lines intersect at point E.
Since point E is satisfied by the equations of both the lines, E is the solution of the given system of equations.
As is evident from the graph, area bounded by the lines and x-axis is the area of $\Delta \text{EBD}$
Here E (2,4), B (-1,0) and D (5,0).
We know that area of $\Delta =\dfrac{1}{2}base\times height$
Length of altitude from E to base BD = ordinate of E = 4
Length of BD = \[5-\left( -1 \right)\text{ }=\text{ }5+1\text{ }=\text{ }6\]
Using the formula of area of triangle in $\Delta \text{EBD}$ we get
Hence area of $\Delta \text{EBD}$ = $\dfrac{1}{2}BD\times y-\text{coordinate of E}$ = $\dfrac{1}{2}\times 6\times 4$=$\dfrac{24}{2}=12$
Note: Equation of line in intercept form is
$\dfrac{x}{a}+\dfrac{y}{b}=1$
This line passes through (a, 0) and (0, b)
So, we can directly find these points by writing the equation in intercept form.
e.g. $4x-3y+4=0$
$\begin{align}
& \Rightarrow 4x-3y=-4 \\
& \Rightarrow \dfrac{4x}{-4}-\dfrac{3y}{-4}=1 \\
\end{align}$
i.e. $\dfrac{x}{-1}+\dfrac{y}{\dfrac{4}{3}}=1$
Hence a = -1 and b = $\dfrac{4}{3}$
Hence the line passes through (-1,0) and $\left( 0,\dfrac{4}{3} \right)$
Complete step-by-step answer:
For equation $4x-3y+4=0$
When x = 0 we have $4\times 0-3y+4=0$
$\begin{align}
& \Rightarrow -3y+4=0 \\
& \Rightarrow -3y=0-4 \\
& \Rightarrow -3y=-4 \\
& \Rightarrow y=\dfrac{-4}{-3} \\
\end{align}$
i.e. $y=\dfrac{4}{3}$
When y = 0 we have $4x-3\times 0+4=0$
$\begin{align}
& \Rightarrow 4x-0+4=0 \\
& \Rightarrow 4x+4=0 \\
& \Rightarrow 4x=-4 \\
& \Rightarrow x=\dfrac{-4}{4} \\
\end{align}$
i.e. $x=-1$
| x | y |
| 0 | $\dfrac{4}{3}$ |
| -1 | 0 |
We plot the points A $\left( 0,\dfrac{4}{3} \right)$ and B$\left( -1,0 \right)$ and draw a line through the points.

So, we have AB $\equiv 4x-3y+4=0$
For equation $4x+3y-20=0$
When x = 0, $4\times 0+3y-20=0$
$\begin{align}
& \Rightarrow 0+3y-20=0 \\
& \Rightarrow 3y-20=0 \\
& \Rightarrow 3y=20 \\
& \Rightarrow y=\dfrac{20}{3} \\
\end{align}$
i.e. $y=\dfrac{20}{3}$
When y = 0, we have $4x+3\times 0-20=0$
$\begin{align}
& \Rightarrow 4x+0-20=0 \\
& \Rightarrow 4x=20 \\
& \Rightarrow 4x=20 \\
& \Rightarrow x=\dfrac{20}{4} \\
\end{align}$
i.e. $x=5$
| x | y |
| 0 | $\dfrac{20}{3}$ |
| 5 | 0 |
We plot points C $\left( 0,\dfrac{20}{3} \right)$ and D \[\left( 5,0 \right)\] and draw line CD on the same graph.
So, CD $\equiv 4x+3y-20=0$

These lines intersect at point E.
Since point E is satisfied by the equations of both the lines, E is the solution of the given system of equations.
As is evident from the graph, area bounded by the lines and x-axis is the area of $\Delta \text{EBD}$
Here E (2,4), B (-1,0) and D (5,0).
We know that area of $\Delta =\dfrac{1}{2}base\times height$
Length of altitude from E to base BD = ordinate of E = 4
Length of BD = \[5-\left( -1 \right)\text{ }=\text{ }5+1\text{ }=\text{ }6\]
Using the formula of area of triangle in $\Delta \text{EBD}$ we get
Hence area of $\Delta \text{EBD}$ = $\dfrac{1}{2}BD\times y-\text{coordinate of E}$ = $\dfrac{1}{2}\times 6\times 4$=$\dfrac{24}{2}=12$
Note: Equation of line in intercept form is
$\dfrac{x}{a}+\dfrac{y}{b}=1$
This line passes through (a, 0) and (0, b)
So, we can directly find these points by writing the equation in intercept form.
e.g. $4x-3y+4=0$
$\begin{align}
& \Rightarrow 4x-3y=-4 \\
& \Rightarrow \dfrac{4x}{-4}-\dfrac{3y}{-4}=1 \\
\end{align}$
i.e. $\dfrac{x}{-1}+\dfrac{y}{\dfrac{4}{3}}=1$
Hence a = -1 and b = $\dfrac{4}{3}$
Hence the line passes through (-1,0) and $\left( 0,\dfrac{4}{3} \right)$
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




