Answer
Verified445.2k+ views
Hint: First of all with the help of the given data, draw the diagram cylinder inscribed in the sphere. Then use the formula for the volume of the cylinder, $ V = \pi {R^2}h $ and use appropriate derivatives to find out the maximum volume inscribed in the given radius.
Complete step-by-step answer:
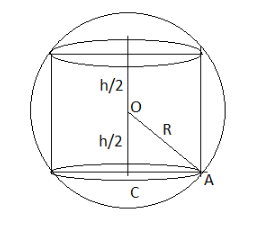
Let us consider the height of the inscribed cylinder is \[ = h\]
And the base radius of the inscribed cylinder be $ = r $
Now, in the above figure $ \Delta OAC, $
By following the Pythagoras theorem –
$ O{C^2} + C{A^2} = O{A^2} $
Place the values in the above equation –
$ \Rightarrow {\left( {\dfrac{h}{2}} \right)^2} + {R^2} = {(5\sqrt 3 )^2} $
Simplify the above equation –
$ \Rightarrow \left( {\dfrac{{{h^2}}}{4}} \right) + {R^2} = (25 \times 3) $
Make Radius “R” the subject –
$ \Rightarrow {R^2} = 75 - \left( {\dfrac{{{h^2}}}{4}} \right) $ .... (A)
Let “V” be the volume of the cylinder –
$ V = \pi {R^2}h $
Place values in the above equation from the equation (A)
$ \Rightarrow V = \pi \left( {75 - \left( {\dfrac{{{h^2}}}{4}} \right)} \right)h $
Simplify the above equation –
$ \Rightarrow V = \pi \left( {\dfrac{{300 - {h^2}}}{4}} \right)h $
Again simplify –
$ \Rightarrow V = \dfrac{\pi }{4}\left( {300h - {h^3}} \right) $
Now, find the derivative of volume with respect to height “h” on both the sides of the equation -
$ \Rightarrow \dfrac{{dV}}{{dh}} = \dfrac{d}{{dh}}\left( {\dfrac{\pi }{4}\left( {300h - {h^3}} \right)} \right) $
Derivative implies –
$ \Rightarrow \dfrac{{dV}}{{dh}} = \dfrac{\pi }{4}\left( {300 - 3{h^2}} \right) $ .... (B)
Take $ \dfrac{{dV}}{{dh}} = 0 $ in the above equation –
$ \Rightarrow 0 = \dfrac{\pi }{4}\left( {300 - 3{h^2}} \right) $
Simplify the above equation –
$ \Rightarrow 0 = 300 - 3{h^2} $
Find the value of height “h”
$ \Rightarrow 300 = 3{h^2} $
When the term multiplicative on one end is moved to the opposite side then it goes to the denominator.
$ \Rightarrow \dfrac{{300}}{3} = {h^2} $
Common factors from the numerator and the denominator cancel each other.
$ \Rightarrow {h^2} = 100 $
Take square-root on both the sides of the equation –
$ \Rightarrow h = 10 $
Find second derivative of the equation (B)
$ \Rightarrow \dfrac{{{d^2}V}}{{d{h^2}}} = \dfrac{\pi }{4}\left( { - 6h} \right) $
Simplify the above equation –
$ \Rightarrow \dfrac{{{d^2}V}}{{d{h^2}}} = \dfrac{\pi }{2}\left( { - 3h} \right) $
Now, place $ h = 10 $ in the above equation-
$ \Rightarrow \dfrac{{{d^2}V}}{{d{h^2}}} = \dfrac{\pi }{2}\left( { - 3 \times 10} \right) $
Simplification implies –
$ \Rightarrow \dfrac{{{d^2}V}}{{d{h^2}}} = - 15\pi < 0 $
Since V is maximum when $ h = 10 $
Therefore, the greatest volume $ = \dfrac{\pi }{4}(300 - 100)(10) $
Simplify the above equation –
$ \therefore $ Volume $ = 500\pi \;c{m^3} $
Hence proved.
Note: Know the difference between the inscribed and circumscribed of the objects and apply accordingly. Inscribed figure is the shape drawn inside another shape whereas, the circumscribed is the shape drawn outside another shape.
Complete step-by-step answer:
Let us consider the height of the inscribed cylinder is \[ = h\]
And the base radius of the inscribed cylinder be $ = r $
Now, in the above figure $ \Delta OAC, $
By following the Pythagoras theorem –
$ O{C^2} + C{A^2} = O{A^2} $
Place the values in the above equation –
$ \Rightarrow {\left( {\dfrac{h}{2}} \right)^2} + {R^2} = {(5\sqrt 3 )^2} $
Simplify the above equation –
$ \Rightarrow \left( {\dfrac{{{h^2}}}{4}} \right) + {R^2} = (25 \times 3) $
Make Radius “R” the subject –
$ \Rightarrow {R^2} = 75 - \left( {\dfrac{{{h^2}}}{4}} \right) $ .... (A)
Let “V” be the volume of the cylinder –
$ V = \pi {R^2}h $
Place values in the above equation from the equation (A)
$ \Rightarrow V = \pi \left( {75 - \left( {\dfrac{{{h^2}}}{4}} \right)} \right)h $
Simplify the above equation –
$ \Rightarrow V = \pi \left( {\dfrac{{300 - {h^2}}}{4}} \right)h $
Again simplify –
$ \Rightarrow V = \dfrac{\pi }{4}\left( {300h - {h^3}} \right) $
Now, find the derivative of volume with respect to height “h” on both the sides of the equation -
$ \Rightarrow \dfrac{{dV}}{{dh}} = \dfrac{d}{{dh}}\left( {\dfrac{\pi }{4}\left( {300h - {h^3}} \right)} \right) $
Derivative implies –
$ \Rightarrow \dfrac{{dV}}{{dh}} = \dfrac{\pi }{4}\left( {300 - 3{h^2}} \right) $ .... (B)
Take $ \dfrac{{dV}}{{dh}} = 0 $ in the above equation –
$ \Rightarrow 0 = \dfrac{\pi }{4}\left( {300 - 3{h^2}} \right) $
Simplify the above equation –
$ \Rightarrow 0 = 300 - 3{h^2} $
Find the value of height “h”
$ \Rightarrow 300 = 3{h^2} $
When the term multiplicative on one end is moved to the opposite side then it goes to the denominator.
$ \Rightarrow \dfrac{{300}}{3} = {h^2} $
Common factors from the numerator and the denominator cancel each other.
$ \Rightarrow {h^2} = 100 $
Take square-root on both the sides of the equation –
$ \Rightarrow h = 10 $
Find second derivative of the equation (B)
$ \Rightarrow \dfrac{{{d^2}V}}{{d{h^2}}} = \dfrac{\pi }{4}\left( { - 6h} \right) $
Simplify the above equation –
$ \Rightarrow \dfrac{{{d^2}V}}{{d{h^2}}} = \dfrac{\pi }{2}\left( { - 3h} \right) $
Now, place $ h = 10 $ in the above equation-
$ \Rightarrow \dfrac{{{d^2}V}}{{d{h^2}}} = \dfrac{\pi }{2}\left( { - 3 \times 10} \right) $
Simplification implies –
$ \Rightarrow \dfrac{{{d^2}V}}{{d{h^2}}} = - 15\pi < 0 $
Since V is maximum when $ h = 10 $
Therefore, the greatest volume $ = \dfrac{\pi }{4}(300 - 100)(10) $
Simplify the above equation –
$ \therefore $ Volume $ = 500\pi \;c{m^3} $
Hence proved.
Note: Know the difference between the inscribed and circumscribed of the objects and apply accordingly. Inscribed figure is the shape drawn inside another shape whereas, the circumscribed is the shape drawn outside another shape.