Question

Prove the theorem: Let $f$ be a differentiable function in a nbd of a point $a$.
(i) If $f'\left( a \right)=0$ and $f'\left( x \right)>0$ in a deleted nbd of $a$ then $f$ is increasing at $a$.

Answer 1

Hint: We will start by using the conditions to be satisfied by a function which is differentiable at any point, when it is continuous at that point:
$\begin{align}
  & f'\left( {{a}^{+}} \right)=\displaystyle \lim_{h \to 0}\dfrac{f\left( a+h \right)-f\left( a \right)}{h}=finite \\
 & f'\left( {{a}^{-}} \right)=\displaystyle \lim_{h \to 0}\dfrac{f\left( a-h \right)-f\left( a \right)}{h}=finite \\
\end{align}$ , where $h \to positive$
$f'\left( {{a}^{+}} \right)=f'\left( {{a}^{-}} \right)=f'\left( a \right)=finite~~value$ , when the function is differentiable at point $a$.

Complete step-by-step solution
Since we have conditions given as $f'\left( x \right)>0$, we will apply this and form two equations for a positive and negative value of h. Then, we will use $f'\left( a \right)=0$ in the equation formed for the positive value of h to conclude the theorem.
Let $f$ is a function, which is continuous and differentiable in the neighborhood of point $a$ and at point $a$ also.

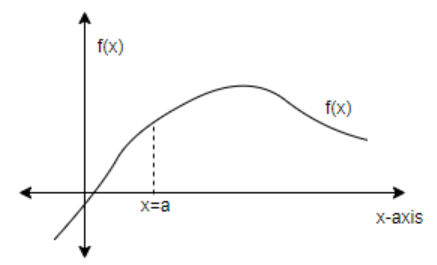
As we know that a function is differentiable at any point, when it is continuous at that point and following condition satisfies –
$\begin{align}
  & f'\left( {{a}^{+}} \right)=\displaystyle \lim_{h \to 0}\dfrac{f\left( a+h \right)-f\left( a \right)}{h}=finite \\
 & f'\left( {{a}^{-}} \right)=\displaystyle \lim_{h \to 0}\dfrac{f\left( a-h \right)-f\left( a \right)}{h}=finite \\
\end{align}$ , where $h \to positive$
And when $f'\left( {{a}^{+}} \right)=f'\left( {{a}^{-}} \right)=f'\left( a \right)=finite~~value$, then function is differentiable at point $a$.
According to definition of differentiability,
\[f'\left( a \right)=\displaystyle \lim_{h \to 0}\dfrac{f\left( a+h \right)-f\left( a \right)}{h}\] , where $h$ may be positive or negative both.
Now in theorem point $a$ is removed, means we cannot put value of $x$ as $a$ in given function $f\left( x \right)$.
So, let the curve of given function be $f\left( x \right)$. Given $f'\left( a \right)=0$ and $f'\left( x \right)>0$.
We know that, \[f'\left( a \right)=\displaystyle \lim_{h \to 0}\dfrac{f\left( a+h \right)-f\left( a \right)}{h}>0\] .
If we take $h$ as positive,
\[\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{f\left( x+h \right)-f\left( x \right)}{h}>0\]
\[\Rightarrow f\left( x+h \right)-f\left( x \right)>0\]
\[\Rightarrow f\left( x+h \right)>f\left( x \right).......(i)\]
It means that if we increase the value of $x$, then value of function is also increasing.
Now, if we take $h$ as negative,
\[\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{f\left( x+h \right)-f\left( x \right)}{h}>0\]
\[\Rightarrow f\left( x+h \right)-f\left( x \right)< 0\]
\[\Rightarrow f\left( x+h \right)< f\left( x \right).......(ii)\]
Here, $h$ is negative, means that if we decrease the value of $x$, then the value of function is also decreasing.
So, according to these relations, curve of given $f\left( x \right)$ will be –

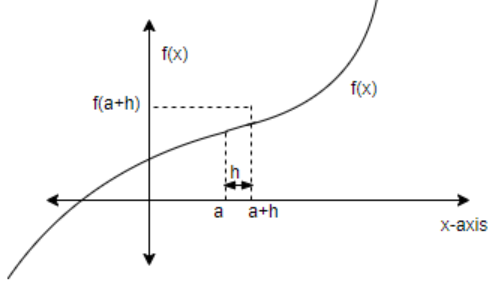
Here, $f'\left( a \right)=0$
In equation (i), where $h>0$, put $x=a$ .
\[\begin{align}
  & \Rightarrow f\left( x+h \right)>f\left( x \right) \\
 & \Rightarrow f\left( a+h \right)>f\left( a \right) \\
\end{align}\]
So, in this function, if we increase $x$, then $f\left( x \right)$ will increase. So it is an increasing function.

Note: Let us take an example of \[f\left( x \right)={{x}^{3}}\]. This is differentiable in nbd of point $a=0$. We remove point $x=0$ from this.

\[f\left( x \right)={{x}^{3}}\]
We differentiate it with respect to $x$.
\[f'\left( x \right)=3{{x}^{2}}\], which is always positive except $x=0$. At $x=0,f'\left( x \right)=0$.
So, $f'\left( 0 \right)=0$, and $f'\left( x \right)>0$ for $x\in R-\left\{ 0 \right\}$.
Hence, \[f\left( x \right)={{x}^{3}}\] is an increasing function.