Question

Prove that \[{{r}_{1}}{{r}_{2}}{{r}_{3}}=r{{s}^{2}}\], where \[{{r}_{1}},{{r}_{2}}\]and \[{{r}_{3}}\]is the radius of the exterior circle on side A, B and C.

Answer 1

Hint: Use heron’s formula to solve. Multiply the radius of these circles considered to prove it. Find the radius of \[{{r}_{1}},{{r}_{2}}\]and \[{{r}_{3}}\]. Prove the LHS by multiplying \[{{r}_{1}},{{r}_{2}}\]and \[{{r}_{3}}\]..


Complete step-by-step answer:
Let us consider that \[{{r}_{1}},{{r}_{2}}\]and \[{{r}_{3}}\]are radius of the circle, opposite to a, b and c of the triangle ABC.
Let the triangle be the area of the triangle ABC.
S is the sum of the length of the triangle ABC.
\[\therefore s=\dfrac{a+b+c}{2}\]
Radius of the triangle, \[r=\dfrac{area}{sum-opposite side}\]
\[\therefore \]radius of \[{{r}_{1}}=\dfrac{\Delta }{s-a}\]
Similarly, \[{{r}_{2}}=\dfrac{\Delta }{s-b}\]and \[{{r}_{3}}=\dfrac{\Delta }{s-c}\]
\[{{r}_{1}}{{r}_{2}}{{r}_{3}}=\left( \dfrac{\Delta }{s-a} \right)\left( \dfrac{\Delta }{s-b} \right)\left( \dfrac{\Delta }{s-c} \right)\]
Where radius \[{{r}_{1}}\]is opposite to the side ‘a’ of \[\vartriangle ABC\]
radius \[{{r}_{2}}\]is opposite to the side ‘b’ of \[\vartriangle ABC\]
radius \[{{r}_{3}}\]is opposite to the side ‘c’ of \[\vartriangle ABC\]
\[\therefore {{r}_{1}}{{r}_{2}}{{r}_{3}}=\dfrac{{{\Delta }^{3}}}{\left( s-a \right)\left( s-b \right)\left( s-c \right)}-(1)\]
By using, Heron’s formula, we can take the area of the triangle, when the length of all three sides of triangle are known:
\[\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}-(2)\]
The figure shows the geometrical significance of \[\left( s-a \right),\left( s-b \right)\]and \[\left( s-c \right)\].
 

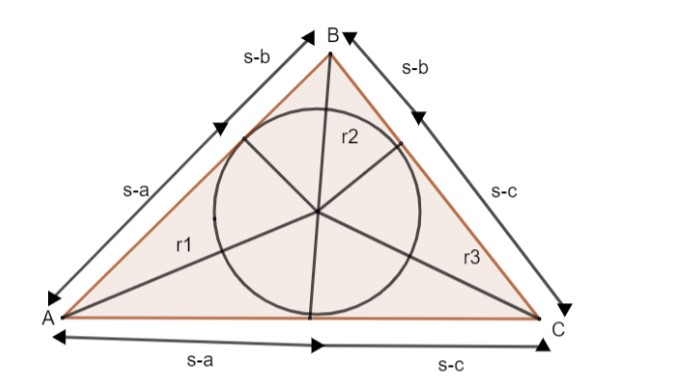
In equation (1) multiply the numerator & denominator by ‘s’.
\[{{r}_{1}}{{r}_{2}}{{r}_{3}}=\dfrac{{{\Delta }^{3}}\times s}{s\times \left( s-a \right)\left( s-b \right)\left( s-c \right)}-(3)\]
We know, \[\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}\]
Squaring equation (2) on both sides
\[{{\Delta }^{2}}=s\left( s-a \right)\left( s-b \right)\left( s-c \right)-(4)\]
Substitute the value of (4) in (3)
\[=\dfrac{s{{\Delta }^{3}}}{{{\Delta }^{2}}}=s\Delta -(5)\]
Multiply numerator and denominator by ‘s’ in equation (5)
\[={{s}^{2}}\dfrac{\Delta }{s}\]
We know the radius in circle, r = a / (sum of lengths of triangle) = \[\dfrac{a}{s}\]
By substituting the same, we get
 \[{{r}_{1}}{{r}_{2}}{{r}_{3}}=r{{s}^{2}}\].
Note: Remember to use heron’s formula to simplify equation (1).