Question

Prove by using vector
\[\cos \left( {\alpha - \beta } \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \]

Answer 1

Hint: It is sometimes useful to write a vector $v$ in terms of its magnitude and argument rather than rectangular form \[a\widehat i + b\widehat j\]. This is done using the sine and cosine functions. The \[r(\cos \alpha \widehat i + \sin \alpha \widehat j)\] version of $v$ is called trigonometric form. Since \[\,\left| {\cos \alpha \widehat i + \sin \alpha \widehat j} \right| = 1\] the trigonometric form expresses $v$ as a scalar multiple of a unit vector in the same direction as $v$.

Complete step by step solution:
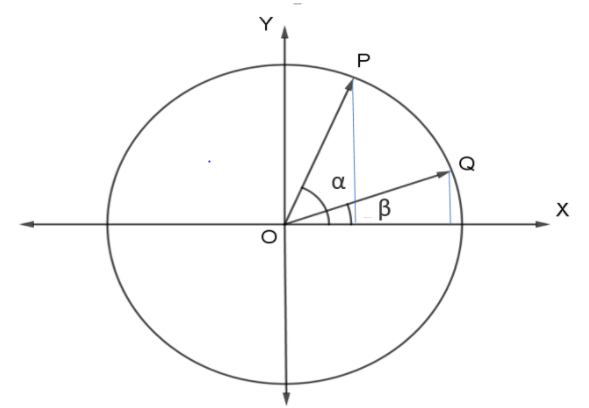
Consider a unit circle.
Draw two-unit vectors \[\overrightarrow {OP} \]and \[\overrightarrow {OQ} \] with an angle of
\[
 \angle POX = \alpha \\
 \angle QOX = \beta \\
 \angle POQ = \alpha - \beta \\
 \]
\[
 \left| {\overrightarrow {OP} } \right| = 1 \\
 \left| {\overrightarrow {OQ} } \right| = 1 \\
 \]
Now as we have described in hint:0
\[
 \overrightarrow {OP} = \cos \alpha \widehat i + \sin \alpha \widehat j \ldots \ldots (1) \\
 \overrightarrow {OQ} = \cos \beta \widehat i + \sin \beta \widehat j \ldots \ldots (2) \\
 \]

The scalar product \[\overrightarrow {OP} \]and \[\overrightarrow {OQ} \]of two vectors \[\overrightarrow {OP} \] and \[\overrightarrow {OQ} \] is a number defined by the equation
\[\overrightarrow {OP} \cdot \overrightarrow {OQ} = \left| {\overrightarrow {OP} } \right|\left| {\overrightarrow {OQ} } \right|\cos \left( {\alpha - \beta } \right) = \cos \left( {\alpha - \beta } \right) \ldots \ldots (3)\]
where \[\alpha \]and \[\beta \] is the angle between the vectors.
Also from equation (1) and (2)
\[
 \overrightarrow {OQ} = \left( {\cos \alpha \widehat i + \sin \alpha \widehat j} \right)\left( {\cos \beta \widehat i + \sin \beta \widehat j} \right) \\
 \Rightarrow \overrightarrow {OP} \cdot \overrightarrow {OQ} = \cos \alpha \widehat i \cdot \cos \beta \widehat i + \cos \alpha \widehat i \cdot \sin \beta \widehat j + \sin \alpha \widehat j \cdot \cos \beta \widehat i + \sin \alpha \widehat j \cdot \sin \beta \widehat j \\
 \Rightarrow \overrightarrow {OP} \cdot \overrightarrow {OQ} = \cos \alpha \widehat i \cdot \sin \beta \widehat j + \sin \alpha \widehat j \cdot \cos \beta \widehat i \\
 \Rightarrow \overrightarrow {OP} \cdot \overrightarrow {OQ} = \cos \alpha \cdot \sin \beta + \sin \alpha \cdot \cos \beta \ldots \ldots (4) \\
 \]
So with the equation (3) and (4)
\[ \Rightarrow \cos \left( {\alpha - \beta } \right) = \cos \alpha \cdot \sin \beta + \sin \alpha \cdot \cos \beta \]

Hence Proved.

Note:
Sometimes people forget when to use sin or cos for calculating vector components. It is important to note that the dot product always results in a scalar value. Furthermore, the dot symbol “.” always refers to a dot product of two vectors, not traditional multiplication of two scalars as we have previously known.