Place A and B are 100km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of two cars?
Answer
Verified360.6k+ views
Hint: First of all, consider the speed of Car A and Car B as SA and SB respectively. When they are moving in the same direction, use (SA – SB)$=\dfrac{\text{Distance between them}}{\text{Time taken by them to meet}}$.
Complete step-by-step answer:
When they are moving in opposite directions, use (SA + SB)$=\dfrac{\text{Distance between them}}{\text{Time taken by them to meet}}$. Solve these two equations to find SA and SB.
We are given that place A and B are 100km apart. Also A and B starts at same time from positions A and B respectively. When they move in the same direction, they meet in 5 hours and when they move in opposite directions, that is, towards each other, they meet in 1 hour. We have to find the speeds of Car A and Car B.
Let us diagrammatically consider the situation,
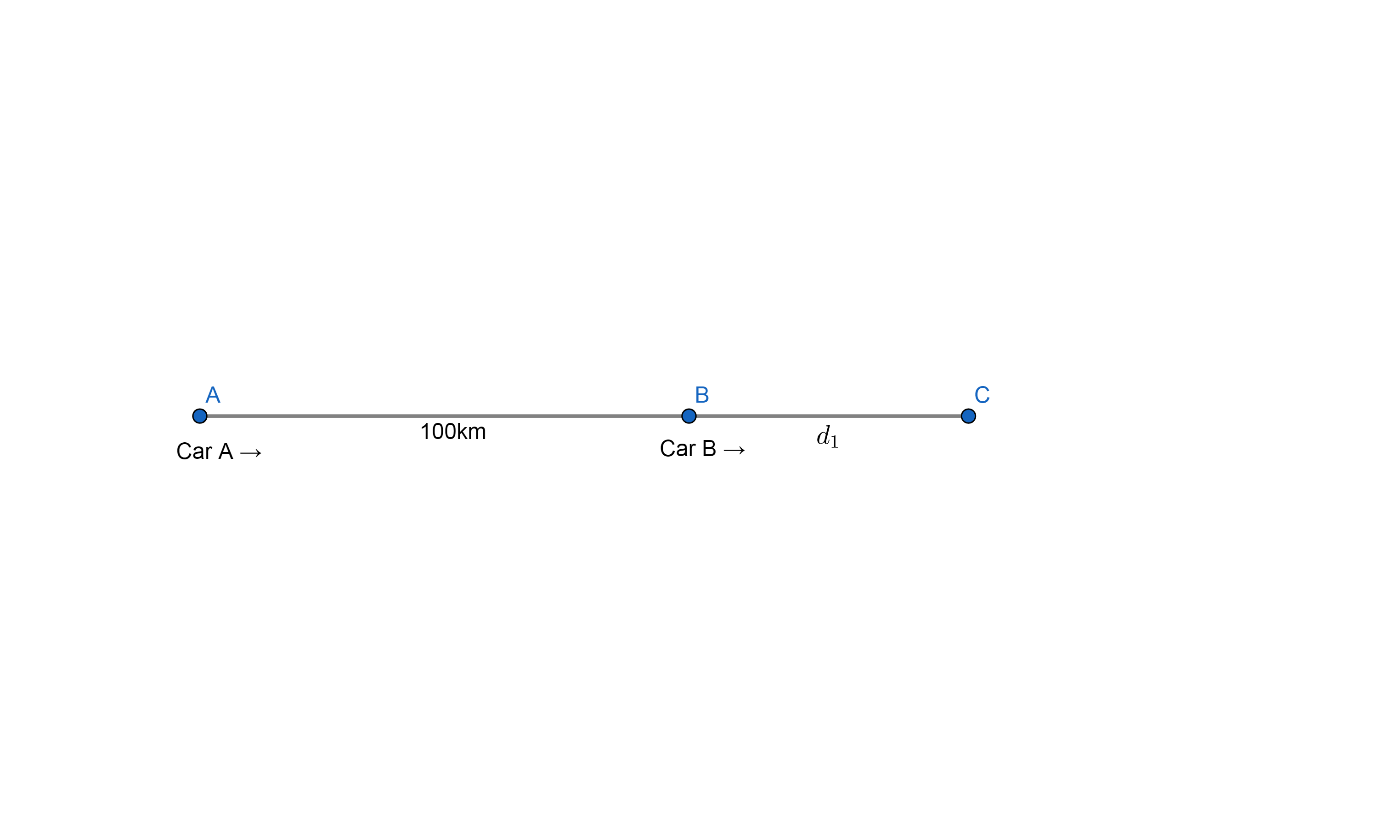
Case I: When both cars are moving in the same direction.
Let us consider that, these cars meet at point C.
Let BC=${{d}_{1}}$
Let the speed of Car A is SA and speed of Car B is SB.
In this case, we are given that Car A and Car B meet after 5 hours. Since they meet at C, therefore this means that Car A takes 5 hours to reach C and Car B also takes 5 hours to reach C. Hence we get,
Time taken by car A to reach C = Time taken by Car B to reach C = 5 hours
As we know that time taken $=\dfrac{\text{Distance travelled}}{\text{Speed}}$ .
Therefore, we get time taken by Car A to reach C $=\dfrac{\text{Distance travelled by car A}}{\text{Speed of car A}}$ .
By putting the value of distance travelled = AB +BC.
$=100+{{d}_{1}}$
Speed of Car A = SA and time taken = 5 hours, we get,
$\dfrac{100+{{d}_{1}}}{SA}=5............\left( 1 \right)$
Also, we get time taken by Car B to reach C $=\dfrac{\text{Distance travelled by car B}}{\text{Speed of car B}}$ .
By putting the value of distance travelled = ${{d}_{1}}$
Speed of Car B = SB and time taken = 5 hours, we get,
$\dfrac{{{d}_{1}}}{SB}=5$
By cross multiplying above equation, we get,
${{d}_{1}}=5SB$
By putting the value of ${{d}_{1}}$in equation (1), we get,
$\dfrac{100+5SB}{SA}=5$
By cross multiplying above equation, we get,
$\begin{align}
& 100+5SB=5SA \\
& or\ 5SA-5SB=100 \\
\end{align}$
By taking out 5 common in above equation, we get,
SA – SB = 20 …………..(2)
Case II: When cars are moving towards each other or in opposite directions.
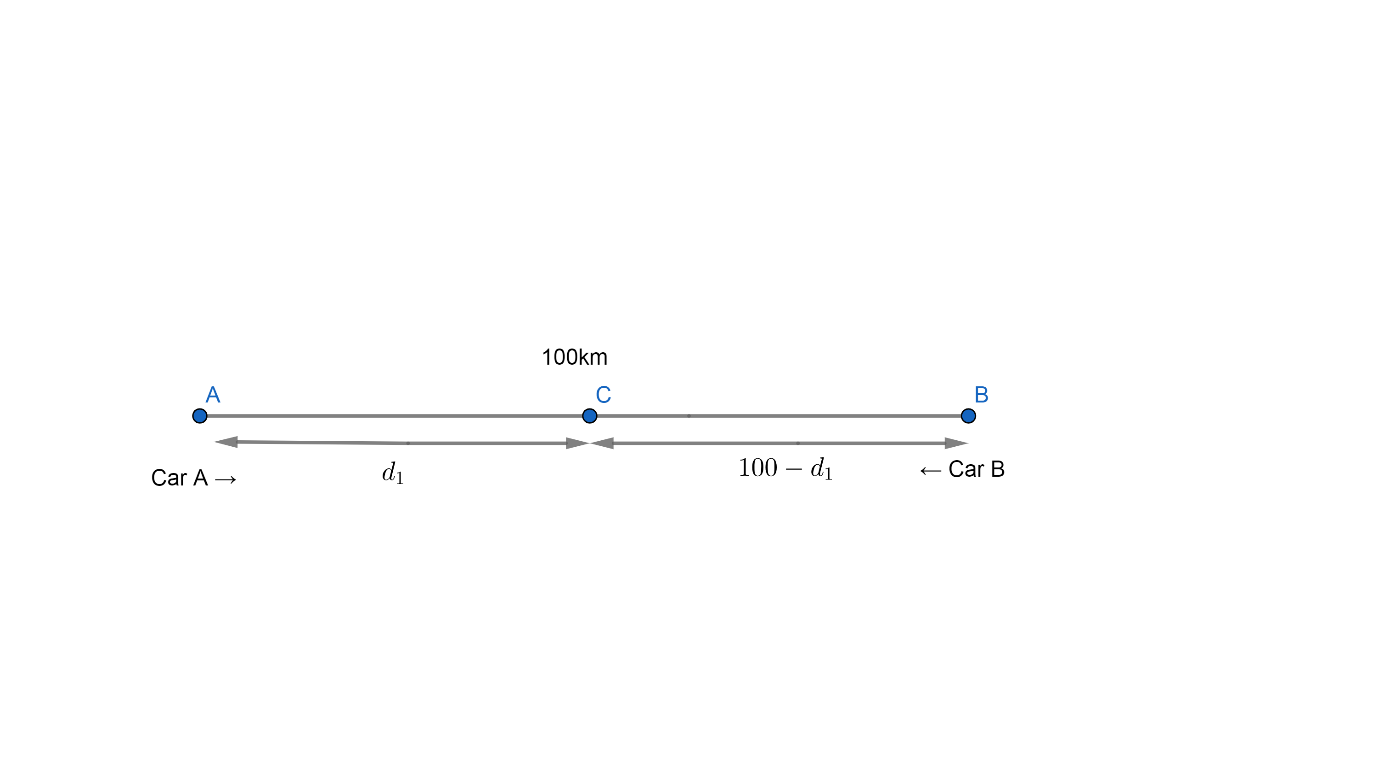
Let us consider that these cars meet at C.
Let AC =${{d}_{1}}$
Since AC + CB = 100km
Therefore, CB = 100 - ${{d}_{1}}$ km
In this case, we are given that Car A and Car B meet after 1 hour
Since they meet at C, therefore this means that Car A takes 1 hour to reach C and Car B also takes 1 hour to reach C. Hence we get,
Time taken by Car A to reach C = Time taken by Car B to reach C = 1 hour
As we know that time taken $=\dfrac{\text{Distance travelled}}{\text{Speed}}$ .
Therefore, we get time taken by Car A to reach C $=\dfrac{\text{Distance travelled by car A}}{\text{Speed of car A}}$.
By putting the value of distance travelled = AC = ${{d}_{1}}$,
Speed of Car A = SA and time taken = 1 hour, we get,
$\dfrac{{{d}_{1}}}{SA}=1$
By cross multiplying above equation, we get,
${{d}_{1}}$= SA ……………… (3)
Also, we get time taken by Car B to reach C $=\dfrac{\text{Distance travelled by car B}}{\text{Speed of car B}}$.
By putting the value of distance travelled = BC = $100-{{d}_{1}}$,
Speed of Car B = SB and time taken = 1 hour, we get,
$\dfrac{100-{{d}_{1}}}{SB}=1$
By cross multiplying above equation, we get,
$\left( 100-{{d}_{1}} \right)=SB$
By putting the value of ${{d}_{1}}$ from equation (3), we get,
(100 – SA) = SB
Or (SA + SB) = 100……………… (4)
By adding equation (2) & (4), we get
(SA + SB) + (SA – SB) = 20 +100
= 2SA = 120
Therefore we get $SA=\dfrac{120}{2}=60km/hr$
By putting the value of SA in equation (4) we get,
60 + SB = 100
SB = 100 – 60 = 40 km/hr
Therefore we get the speed of Car A as 60 km/hr and Car B as 40 km/hr.
Note: Students must note that whenever two cars are moving in the same direction, they will never meet at a point between them. In the same way, if they are moving towards each other, they will always meet at a point between them. Also students can cross check their answer by putting SA and SB back to equations and checking if they are satisfying the equations or not.
Here students can also calculate SA and SB by using direct formula that is $SA=\dfrac{\dfrac{D}{{{T}_{1}}}+\dfrac{D}{{{T}_{2}}}}{2}\ and\ SB=\dfrac{\dfrac{D}{{{T}_{1}}}-\dfrac{D}{{{T}_{2}}}}{2}$ .
Where D is the distance between A and B. ${{T}_{1}}$ is time taken by them to meet when they are moving towards each other and ${{T}_{2}}$is time taken by them to meet when they are moving in same direction.
Complete step-by-step answer:
When they are moving in opposite directions, use (SA + SB)$=\dfrac{\text{Distance between them}}{\text{Time taken by them to meet}}$. Solve these two equations to find SA and SB.
We are given that place A and B are 100km apart. Also A and B starts at same time from positions A and B respectively. When they move in the same direction, they meet in 5 hours and when they move in opposite directions, that is, towards each other, they meet in 1 hour. We have to find the speeds of Car A and Car B.
Let us diagrammatically consider the situation,
Case I: When both cars are moving in the same direction.
Let us consider that, these cars meet at point C.
Let BC=${{d}_{1}}$
Let the speed of Car A is SA and speed of Car B is SB.
In this case, we are given that Car A and Car B meet after 5 hours. Since they meet at C, therefore this means that Car A takes 5 hours to reach C and Car B also takes 5 hours to reach C. Hence we get,
Time taken by car A to reach C = Time taken by Car B to reach C = 5 hours
As we know that time taken $=\dfrac{\text{Distance travelled}}{\text{Speed}}$ .
Therefore, we get time taken by Car A to reach C $=\dfrac{\text{Distance travelled by car A}}{\text{Speed of car A}}$ .
By putting the value of distance travelled = AB +BC.
$=100+{{d}_{1}}$
Speed of Car A = SA and time taken = 5 hours, we get,
$\dfrac{100+{{d}_{1}}}{SA}=5............\left( 1 \right)$
Also, we get time taken by Car B to reach C $=\dfrac{\text{Distance travelled by car B}}{\text{Speed of car B}}$ .
By putting the value of distance travelled = ${{d}_{1}}$
Speed of Car B = SB and time taken = 5 hours, we get,
$\dfrac{{{d}_{1}}}{SB}=5$
By cross multiplying above equation, we get,
${{d}_{1}}=5SB$
By putting the value of ${{d}_{1}}$in equation (1), we get,
$\dfrac{100+5SB}{SA}=5$
By cross multiplying above equation, we get,
$\begin{align}
& 100+5SB=5SA \\
& or\ 5SA-5SB=100 \\
\end{align}$
By taking out 5 common in above equation, we get,
SA – SB = 20 …………..(2)
Case II: When cars are moving towards each other or in opposite directions.
Let us consider that these cars meet at C.
Let AC =${{d}_{1}}$
Since AC + CB = 100km
Therefore, CB = 100 - ${{d}_{1}}$ km
In this case, we are given that Car A and Car B meet after 1 hour
Since they meet at C, therefore this means that Car A takes 1 hour to reach C and Car B also takes 1 hour to reach C. Hence we get,
Time taken by Car A to reach C = Time taken by Car B to reach C = 1 hour
As we know that time taken $=\dfrac{\text{Distance travelled}}{\text{Speed}}$ .
Therefore, we get time taken by Car A to reach C $=\dfrac{\text{Distance travelled by car A}}{\text{Speed of car A}}$.
By putting the value of distance travelled = AC = ${{d}_{1}}$,
Speed of Car A = SA and time taken = 1 hour, we get,
$\dfrac{{{d}_{1}}}{SA}=1$
By cross multiplying above equation, we get,
${{d}_{1}}$= SA ……………… (3)
Also, we get time taken by Car B to reach C $=\dfrac{\text{Distance travelled by car B}}{\text{Speed of car B}}$.
By putting the value of distance travelled = BC = $100-{{d}_{1}}$,
Speed of Car B = SB and time taken = 1 hour, we get,
$\dfrac{100-{{d}_{1}}}{SB}=1$
By cross multiplying above equation, we get,
$\left( 100-{{d}_{1}} \right)=SB$
By putting the value of ${{d}_{1}}$ from equation (3), we get,
(100 – SA) = SB
Or (SA + SB) = 100……………… (4)
By adding equation (2) & (4), we get
(SA + SB) + (SA – SB) = 20 +100
= 2SA = 120
Therefore we get $SA=\dfrac{120}{2}=60km/hr$
By putting the value of SA in equation (4) we get,
60 + SB = 100
SB = 100 – 60 = 40 km/hr
Therefore we get the speed of Car A as 60 km/hr and Car B as 40 km/hr.
Note: Students must note that whenever two cars are moving in the same direction, they will never meet at a point between them. In the same way, if they are moving towards each other, they will always meet at a point between them. Also students can cross check their answer by putting SA and SB back to equations and checking if they are satisfying the equations or not.
Here students can also calculate SA and SB by using direct formula that is $SA=\dfrac{\dfrac{D}{{{T}_{1}}}+\dfrac{D}{{{T}_{2}}}}{2}\ and\ SB=\dfrac{\dfrac{D}{{{T}_{1}}}-\dfrac{D}{{{T}_{2}}}}{2}$ .
Where D is the distance between A and B. ${{T}_{1}}$ is time taken by them to meet when they are moving towards each other and ${{T}_{2}}$is time taken by them to meet when they are moving in same direction.
Last updated date: 24th Sep 2023
•
Total views: 360.6k
•
Views today: 4.60k
Recently Updated Pages
