Questions & Answers
Question
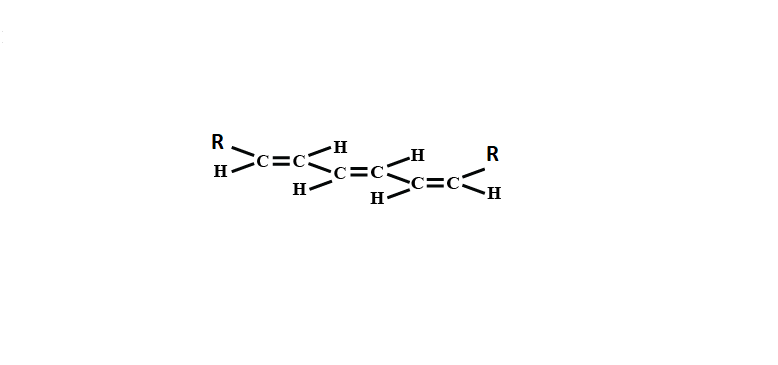
AnswersNumber of geometrical isomers for the molecule
(A).2
(B).4
(C).6
(D).8
Answer
Verified91.5k+ views
Hint: To write the geometrical isomerism we have to identify the bonding connectivity between atoms. The molecules having the same bonding connectivity can be a geometrical isomer.
Complete answer:
The stereoisomers are defined as the molecules have the same bonding connectivity and different molecular configuration. Stereoisomers are of two type’s i.e. optical and geometrical isomers.
Geometrical isomers are the isomers which differ by the arrangement along the double bond ring and other rigid structure.
Given in the above molecule:
3 double bonds which are shown below and the molecule is symmetric:
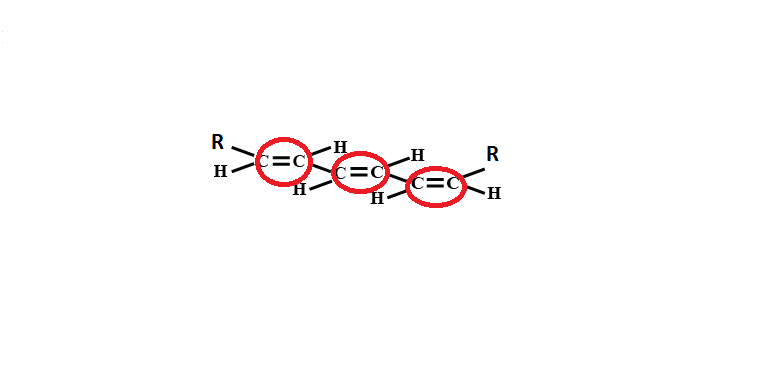
The total number of geometrical isomers will be= ${{2}^{n-1}}+{{2}^{\dfrac{n-1}{2}}}$
Put the value of n =3
\[{{2}^{3-1}}+{{2}^{\dfrac{3-1}{2}}}\]
\[{{2}^{2}}-{{2}^{1}}\]
\[4+2=6\]
Hence the number of geometrical isomers for the molecule is 6.
So, Correct answer is option (C).
Additional information:
Optical isomers are the molecules which differ from each other in their behavior towards the plane-polarized light. They have the different arrangements of the same atoms or groups in a molecule.
Enantiomers are defined as the stereoisomers of a compound which have non superimposable mirror images. They have identical physical properties, the enantiomer which rotates the plane polarized light to the left is known as laevo rotatory and the enantiomer which rotates the plane polarized light to the right is known as dextrorotatory.
Note:
While identifying the geometrical isomers it is important to restrict the rotation of the carbon-carbon double bond. A main criteria of having geometrical isomerism is to have different groups attached to the carbon atoms.
Complete answer:
The stereoisomers are defined as the molecules have the same bonding connectivity and different molecular configuration. Stereoisomers are of two type’s i.e. optical and geometrical isomers.
Geometrical isomers are the isomers which differ by the arrangement along the double bond ring and other rigid structure.
Given in the above molecule:
3 double bonds which are shown below and the molecule is symmetric:
The total number of geometrical isomers will be= ${{2}^{n-1}}+{{2}^{\dfrac{n-1}{2}}}$
Put the value of n =3
\[{{2}^{3-1}}+{{2}^{\dfrac{3-1}{2}}}\]
\[{{2}^{2}}-{{2}^{1}}\]
\[4+2=6\]
Hence the number of geometrical isomers for the molecule is 6.
So, Correct answer is option (C).
Additional information:
Optical isomers are the molecules which differ from each other in their behavior towards the plane-polarized light. They have the different arrangements of the same atoms or groups in a molecule.
Enantiomers are defined as the stereoisomers of a compound which have non superimposable mirror images. They have identical physical properties, the enantiomer which rotates the plane polarized light to the left is known as laevo rotatory and the enantiomer which rotates the plane polarized light to the right is known as dextrorotatory.
Note:
While identifying the geometrical isomers it is important to restrict the rotation of the carbon-carbon double bond. A main criteria of having geometrical isomerism is to have different groups attached to the carbon atoms.