Question

What is the moment of force about the apex of triangle, if 3 forces of 40 N each acting along the sides of equilateral of side 2m taken in order
A. 51.96Nm
B. 69.3Nm
C. 30.6Nm
D. 6.67Nm

Answer 1

Hint: Moment of force or torque about a point is defined as the product of the force and the perpendicular distance of the point from the line of the force. Find the perpendicular distances of the point from each side of the triangle.
Formula used:
$\tau =Fd$

Complete answer:
It is given that three forces with magnitude of 40 N each are acting along the sides of an equilateral triangle in order. It is said that each side of the triangle is equal to 2m. This can be seen in the given figure below.

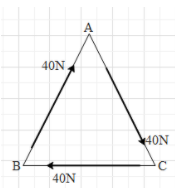
Then we are asked to find the moment of force about the apex of the triangle, i.e. is vertex A.
Moment of force at a point is also called torque about that point. The magnitude of torque is given as $\tau =Fd$ ….. (i),
where F is the force and d is the perpendicular distance of the point from the line of the force.
From this definition of torque we understand that the torque about point A due to the forces along sides AB and AC is zero, since the perpendicular distance of A from the lines of these forces is zero.

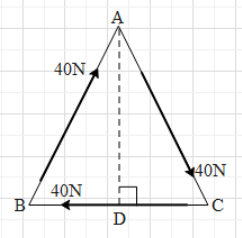
Let us calculate the perpendicular distance of the point A from the force along the side BC. Form the figure we get to know that it is equal to AD.
AD will bisect the side BC. Therefore, BD=DC=1m
 The $\Delta ADB$ is a right angled triangle. Therefore, $A{{B}^{2}}=A{{D}^{2}}+B{{D}^{2}}$.
 $\Rightarrow {{2}^{2}}=A{{D}^{2}}+{{1}^{2}}$
$\Rightarrow A{{D}^{2}}={{2}^{2}}-{{1}^{2}}=4-1=3$
$\Rightarrow AD=\sqrt{3}m$
Now, substitute $d=\sqrt{3}$ and F = 40N in equation (i).
$\tau =40\sqrt{3}=69.3m$.
Hence, the torque about the apex of the triangle is 69.3m.

Hence, the correct option is B.

Note:
Note that torque about a point is a vector quantity. This means that the direction of torque must be taken into consideration.
When the moment of force produces a rotation in clockwise direction, the torque is taken as positive. When the moment of force produces a rotation in anticlockwise direction, the torque is taken as negative.