Question

What is the Mirror formula? Derive the relation $\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{2}{R}$ for a concave mirror.

Answer 1

Hint: Mirror formula is an equation that relates the distance of the object and distance of the image to the focal length of the mirror, and hence to the radius of curvature of the mirror, since, focal length is half of the radius of curvature of the mirror.

Complete answer:
Mirror formula or mirror equation relates the distance of the object from the pole of the mirror ’u’ and distance of the image from the pole of the mirror ‘v’ and the focal length ‘f’ of the mirror. The diagram below shows a concave mirror,

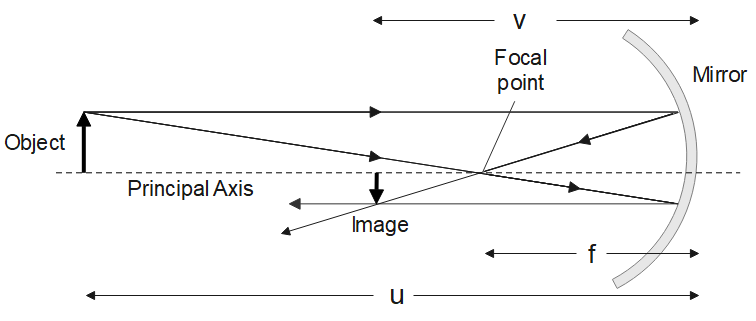
Mirror formula is given by,
$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$ ….(i)
Where, u is distance of the object from the pole of the mirror and v is distance of the image from the pole of the mirror and f is the focal length of the mirror.
Derivation:
Let us consider an object AB, the image of the object AB is A’B’ as shown in the figure below. Point F is the focal point. When measuring distances, if direction is opposite to that of the incident ray then negative and vice versa.

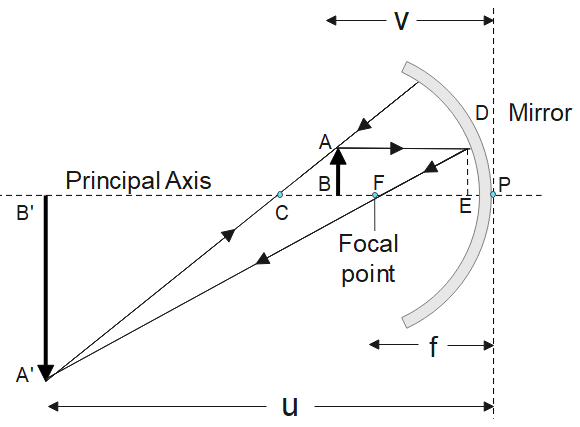
Consider the $\Delta $A’B’C and $\Delta $ABC,
$\Rightarrow \angle A'CB=\angle ACB$ [They are vertically opposite]
$\Rightarrow \angle AB'C=\angle ABC$ [Equal to ${{90}^{0}}$]
$\Rightarrow \angle B'A'C=\angle BAC$ [Third angles are equal since other two are equal]
Therefore, $\Delta $A’B’C and $\Delta $ABC are similar triangles.
Hence, we can write,
$\dfrac{A'B'}{AB}=\dfrac{B'C}{BC}$ ….(ii)
Similarly, $\Delta $FB’A’ and $\Delta $FED are similar triangles, hence we can write,
$\dfrac{A'B'}{ED}=\dfrac{FB'}{EF}$
$\Rightarrow \dfrac{A'B'}{AB}=\dfrac{FB'}{EF}$ ….(iii) [Since,$ED=AB$]
Now comparing equation (ii) and (iii),we get,
$\dfrac{B'C}{BC}=\dfrac{FB'}{EF}\Rightarrow \dfrac{BC}{B'C}=\dfrac{EF}{FB'}$ ….(iv)
If we consider that point P and D are close to each other then,
$EF=PF$
So equation (iv) becomes,
$\dfrac{BC}{B'C}=\dfrac{PF}{FB'}$ ….(v)
$\Rightarrow \dfrac{(PC-PB)}{(PB'-PC)}=\dfrac{PF}{(PB'-PF)}$ ….(vi) [Since, $BC=PC-PB$,$B'C=PB'-PC$and $FB'=PB'-PF$)
Also,$PC=-R,PB=u,PB'=-v$and $PF=-f$ from the diagram.
Putting the above values in equation (vi) and solving, we get,
$\dfrac{(u-R)}{(R-v)}=\dfrac{f}{(v-f)}$
Cross multiplying and simplifying,
$uv-Rv-uf+vf=0$
Now, substituting $f=\dfrac{R}{2}$ and solving , as focal length is half of the centre of curvature, we get,
$uv-\dfrac{uR}{2}-\dfrac{vR}{2}=0$
Multiplying the above by 2 and dividing it by $uvR$, we get,
$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{2}{R}$
Hence, the above equation is the mirror formula for concave mirrors.

Note:
The general equation of the mirror formula is important to remember, the mirror formula can be used to calculate the value of focal length if u and v is given. The radius of curvature is equal to twice the focal length of the mirror.