Answer
Verified444.3k+ views
Hint: Meiosis is known as reductional division because the chromosome number becomes half after this division whereas mitosis is known as equational division because the chromosome number remains the same even after the division.
Complete answer:
Mendel’s Laws of Heredity consists of three laws known as the Law of Dominance, the Law of Segregation, and the Law of Independent Assortment. These laws can be explained with the help of meiosis. It is a type of cell division that takes place during gamete formation as the number of chromosomes gets halved in this.
The Law of Dominance states that there in the case of the heterozygous condition, the dominant allele expresses itself, which is explained by meiosis as, during fertilization of gametes, the heterozygous condition may occur.
The Law of Segregation states that during gamete formation, two alleles separate, and one each is present in a gamete. This is in accordance with meiosis as two chromosomes separate out in which the allele is present during this process.
The Law of Independent Assortment states that two genes assort independently of each other which is explained by meiosis as two different chromosomes separate out independent of each other during meiosis.
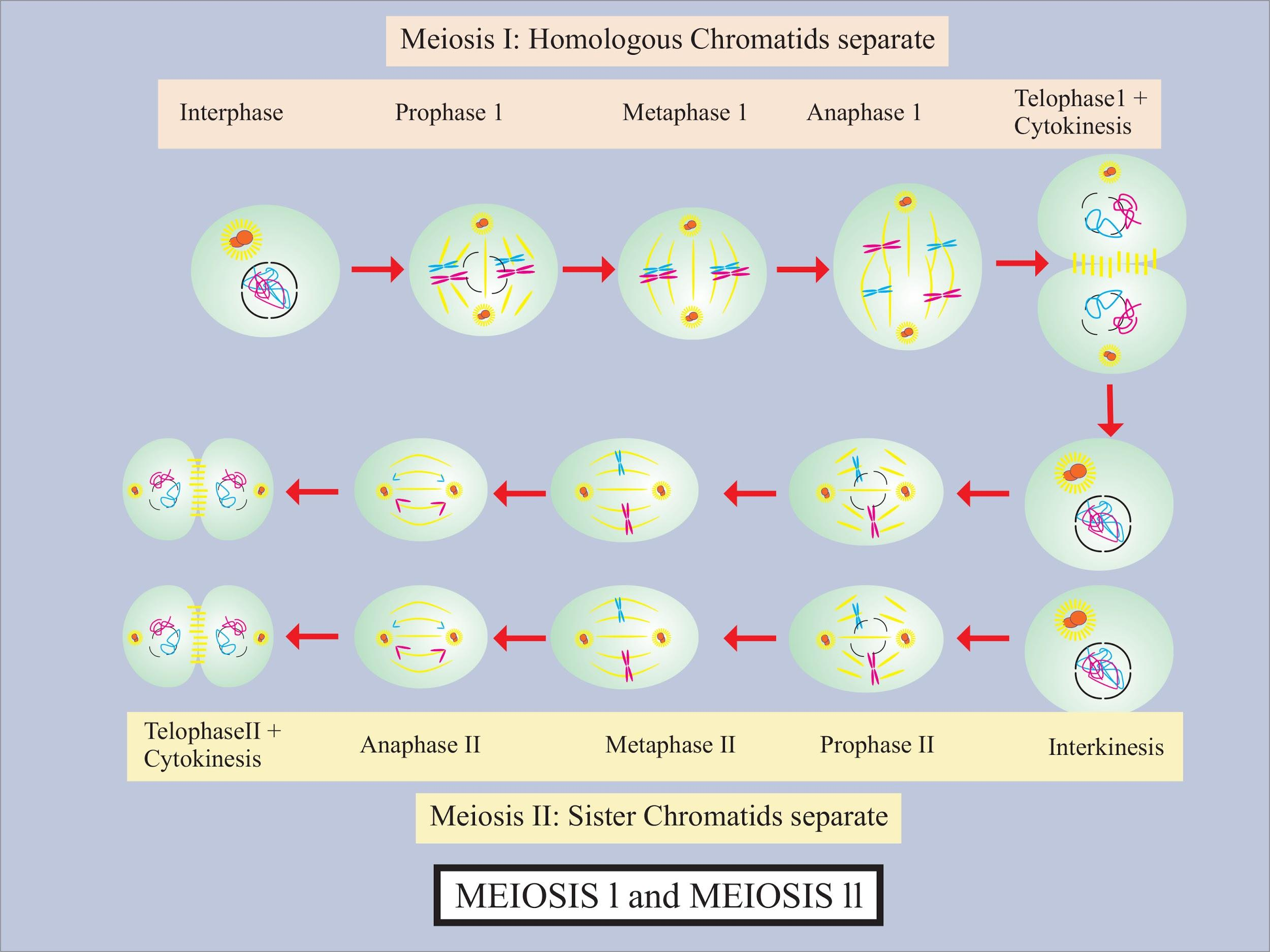
Additional Information: Let us look at the process of meiosis in detail. It is divided into
Meiosis-I: This is further divided into
(a)Prophase-I: It consists of 5 phases known as leptotene, zygotene, pachytene, diplotene, and diakinesis. In this phase crossing over and recombination of homologous chromosomes occurs.
(b)Metaphase-I: In this phase homologous chromosomes are aligned along the equator known as the metaphase plate.
(c)Anaphase-I: In this phase, homologous chromosomes are separated due to the contraction of spindle fibers.
(d)Telophase-I: Karyokinesis occurs in this phase followed by cytokinesis resulting in 2 cells with half the number of chromosomes.
Meiosis-II: This is further divided into:
(a)Prophase-II: There is a disappearance of the nuclear membrane and condensation of the genetic material.
(b)Metaphase-II: Chromosomes are aligned on the equator again.
(c)Anaphase-II: This time instead of homologous chromosomes, chromatids are separated.
(d)Telophase-II: Karyokinesis takes place followed by cytokinesis.
So, the correct option is ‘Meiosis’.
Note: -Crossing over which leads to recombination takes place in the pachytene stage of prophase-I.
-After crossing over, there are some parts where the homologous chromosomes are still joined which are known as chiasmata.
-Exceptions of the law of dominance is seen in the cases of incomplete dominance and codominance.
Complete answer:
Mendel’s Laws of Heredity consists of three laws known as the Law of Dominance, the Law of Segregation, and the Law of Independent Assortment. These laws can be explained with the help of meiosis. It is a type of cell division that takes place during gamete formation as the number of chromosomes gets halved in this.
The Law of Dominance states that there in the case of the heterozygous condition, the dominant allele expresses itself, which is explained by meiosis as, during fertilization of gametes, the heterozygous condition may occur.
The Law of Segregation states that during gamete formation, two alleles separate, and one each is present in a gamete. This is in accordance with meiosis as two chromosomes separate out in which the allele is present during this process.
The Law of Independent Assortment states that two genes assort independently of each other which is explained by meiosis as two different chromosomes separate out independent of each other during meiosis.
Additional Information: Let us look at the process of meiosis in detail. It is divided into
Meiosis-I: This is further divided into
(a)Prophase-I: It consists of 5 phases known as leptotene, zygotene, pachytene, diplotene, and diakinesis. In this phase crossing over and recombination of homologous chromosomes occurs.
(b)Metaphase-I: In this phase homologous chromosomes are aligned along the equator known as the metaphase plate.
(c)Anaphase-I: In this phase, homologous chromosomes are separated due to the contraction of spindle fibers.
(d)Telophase-I: Karyokinesis occurs in this phase followed by cytokinesis resulting in 2 cells with half the number of chromosomes.
Meiosis-II: This is further divided into:
(a)Prophase-II: There is a disappearance of the nuclear membrane and condensation of the genetic material.
(b)Metaphase-II: Chromosomes are aligned on the equator again.
(c)Anaphase-II: This time instead of homologous chromosomes, chromatids are separated.
(d)Telophase-II: Karyokinesis takes place followed by cytokinesis.
So, the correct option is ‘Meiosis’.
Note: -Crossing over which leads to recombination takes place in the pachytene stage of prophase-I.
-After crossing over, there are some parts where the homologous chromosomes are still joined which are known as chiasmata.
-Exceptions of the law of dominance is seen in the cases of incomplete dominance and codominance.