Question

Let $f:R-\left\{ \dfrac{3}{5} \right\}\to R$ be defined by $f(x)=\dfrac{3x+2}{5x-3}$ . Then,which of the following options are correct?.
A. ${{f}^{-1}}(x)=f(x)$
B. ${{f}^{-1}}(x)=-f(x)$
C. $fof(x)=-x$
D. ${{f}^{-1}}(x)=\dfrac{1}{19}f(x)$

Answer 1

Hint: To find an inverse function such as f(x) we have the following method: Express x in terms of f(x) and then replace x with g(x) and f(x) with x. The resultant function g(x) will be the inverse of the function f(x) then we check which of the options are correct.

“Complete step-by-step answer:”
We have the function $f(x)=\dfrac{3x+2}{5x-3}$ . First of all let us express x in terms of f(x). For that we have,
$f(x)[5x-3]=3x+2$
Multiplying f(x) we have,
$5xf(x)-3f(x)=3x+2$
Taking 3x in LHS and -3f(x) in RHS we have,
$5xf(x)-3x=3f(x)+2$
Taking x common from the terms in LHS we have,
$x(5f(x)-3)=3f(x)+2$
Dividing both sides with coefficient of x we have,
$x=\dfrac{3f(x)+2}{5f(x)-3}$
Now replacing x with g(x) and f(x) with x we have,
$g(x)=\dfrac{3x+2}{5x-3}$
This function g(x) is the inverse of the function f(x). Hence, we can write ${{f}^{-1}}(x)=\dfrac{3x+2}{5x-3}$ .
We had $f(x)=\dfrac{3x+2}{5x-3}$ and ${{f}^{-1}}(x)=\dfrac{3x+2}{5x-3}$ . Therefore $f(x)={{f}^{-1}}(x)$ .
Hence, option A is the correct answer.
Note: We should know that the inverse of a function is a mirror image of the function about the line $y=x$ means if we were to plot the graph of a function and its inverse we will find that they are mirror image of each other about the line $y=x$ .

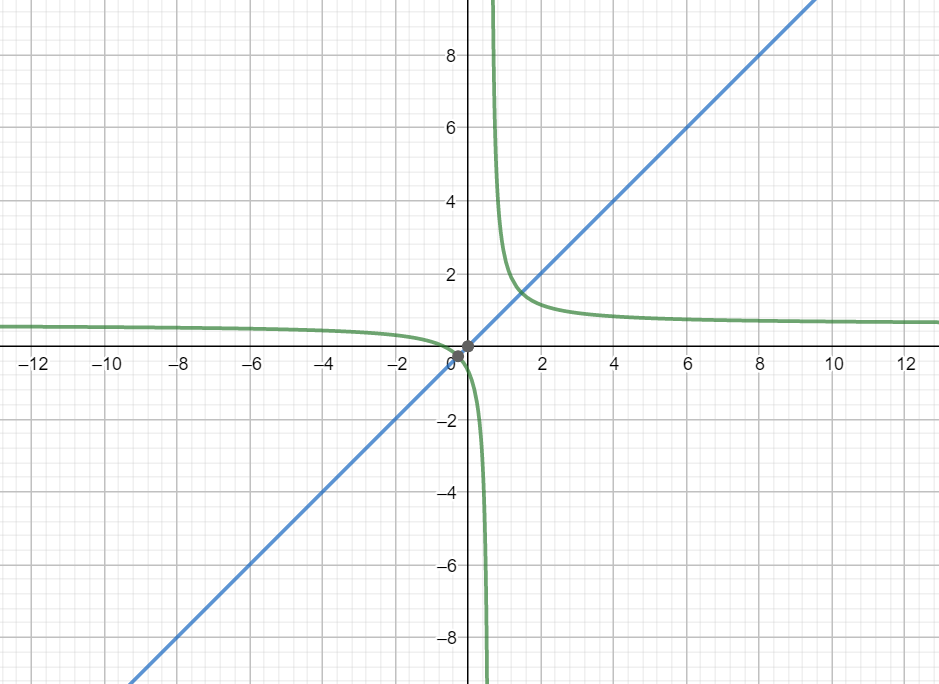
This the graph of the function $f(x)=\dfrac{3x+2}{5x-3}$ . As we can see the function is perfectly symmetric and if we were to draw the mirror image it would again give the same function.