Question

Let ABCD be a square and E be a point outside ABCD such that E,A,C are collinear in that order. Suppose EB=ED=$\sqrt{130}$ and the areas of triangle EAB and square ABCD are equal. Then the area of square ABCD is?
A. 8
B. 10
C. $\sqrt{120}$
D. $\sqrt{125}$

Answer 1

Hint:Find area of triangle EAB in terms of side of square. Use property of square and congruent triangle i.e. congruent triangle have the same area.

Complete step-by-step answer:
Let us draw a diagram by using the given information which are
$*$ABCD is a square and suppose side=a
$*$E is outside and E,A,C are collinear i.e. E,A,C lying on a line
$*$EB=ED=$\sqrt{130}$
$*$Area of triangle EAB=Area of square ABCD

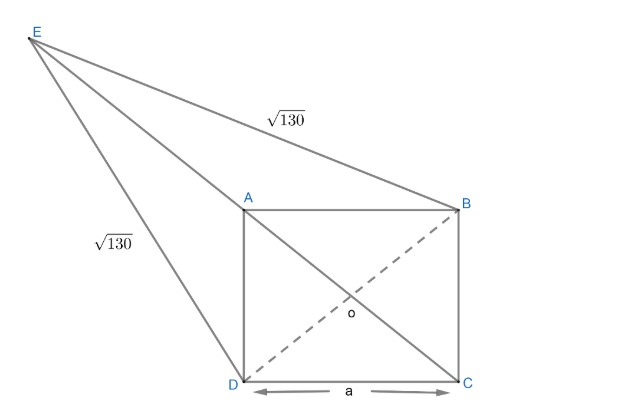
                                                                    Figure 1
On joining BD, we get a triangle DEB with two sides equal, hence it will be an isosceles triangle.

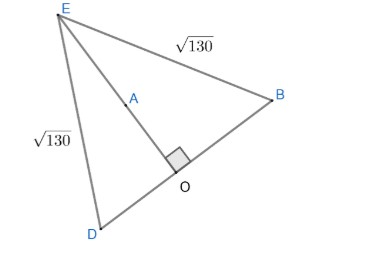
            Figure 2
As E,A,C are collinear, means AC will be one of diagonals of square and BD is another. As we know the property of square that diagonals are perpendicular to each other and bisect each other as well.
As AO is a part of diagonal AC which is perpendicular to BD, it means AO is perpendicular to BD.
Now, coming to figure (2), AO or EO is perpendicular to each other. So, area of any triangle can be written as;
$Area\text{ }of\text{ triangle}=\dfrac{1}{2}\times base\times height$
In triangle BED, we have base =BD and Height=OE
Hence, $Area\text{ }of\text{ }\Delta \text{BED}=\dfrac{1}{2}\times BD\times EO.........\left( 1 \right)$
We can get length BD by using Pythagoras in $\Delta BCD$ from figure (1)

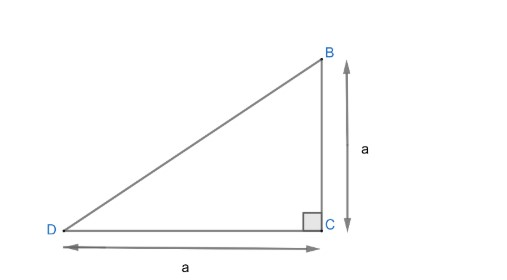
Figure 3
We have,
\[\begin{align}
& {{\left( BD \right)}^{2}}=B{{C}^{2}}+C{{D}^{2}} \\
& {{\left( BD \right)}^{2}}={{a}^{2}}+{{a}^{2}}=2{{a}^{2}} \\
& BD=\sqrt{2a}.....................\left( 2 \right) \\
\end{align}\]
Now, we can calculate EO in triangle EOB by using Pythagoras in following way;

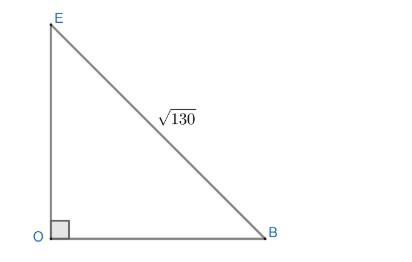
We know,
$OB=\left( \dfrac{BD}{2} \right)$ as BD is bisected by AC at point O
Hence $OB=\dfrac{a\sqrt{2}}{2}(BD=a\sqrt{2})$
Or $OB=\dfrac{2}{\sqrt{2}}$
Now applying Pythagoras in triangle EOB
$\begin{align}
& E{{B}^{2}}=E{{O}^{2}}+O{{B}^{2}} \\
& {{\left( \sqrt{130} \right)}^{2}}=E{{O}^{2}}+{{\left( \dfrac{a}{\sqrt{2}} \right)}^{2}} \\
&E{{O}^{2}}=130-\dfrac{{{a}^{2}}}{2} \\
& EO=\sqrt{130-\dfrac{{{a}^{2}}}{2}}.................\left( 3 \right) \\
\end{align}$
Area of triangle BED from equation (1) is
Area of $\Delta BED$$=\dfrac{1}{2}\times \sqrt{130-\dfrac{{{a}^{2}}}{2}}\sqrt{2a}..........\left( 4 \right)$
Now, we are given that
Area of square = area of $\Delta EAB.............\left( 5 \right)$
We know;
Area of square ${{\left( side \right)}^{2}}$
Here, side is given as ‘a’
Area of square$={{a}^{2}}...................\left( 6 \right)$
We can observe from figure (1) that $\Delta EAD\And \Delta EAB$ are congruent in following manners:
ED=EB=$\sqrt{130}$
AD=AB(sides of square)
EA=EA(common)
Hence, $\Delta EAD\And \Delta EAB$are congruent to each other by SSS property. Therefore, the area of $\Delta EAD$ should be equal to the area of $\Delta EAB$ as the area of congruent triangles are equal.
Now, from figure (1), we can write area of $\Delta EAB$as
Area of $\Delta EAB$=$\left( \dfrac{\text{area of }\Delta BED-\text{area of }\Delta ABD}{2} \right).............\left( 7 \right)$
Area of $\Delta ABD$ can be calculated by basic formula $\dfrac{1}{2}\times base\times height$ where base=BD and height=OA
We have,
BD=$a\sqrt{2}$
$OA=\dfrac{a\sqrt{2}}{2}=\dfrac{a}{\sqrt{2}}$
Area of $\Delta ABD=\dfrac{1}{2}a\sqrt{2}\times \dfrac{a}{\sqrt{2}}=\dfrac{1}{2}{{a}^{2}}.................\left( 8 \right)$
Using equation (7) and (8) and (5) we get area of $\Delta EAB$ as
Area of $\Delta EAB$$=\dfrac{\dfrac{1}{2}\times \sqrt{130-\dfrac{{{a}^{2}}}{2}}\sqrt{2a}-\dfrac{1}{2}{{a}^{2}}}{2}....................\left( 9 \right)$
Now, using equation (5),(6)and (9), we get;
Area of square = area of $\Delta EAB$
$\dfrac{{{a}^{2}}}{1}=\dfrac{\dfrac{1}{2}\times \sqrt{130-\dfrac{{{a}^{2}}}{2}}\sqrt{2a}-\dfrac{{{a}^{2}}}{2}}{2}$
On cross multiplying we get:
\[\begin{align}
& 2{{a}^{2}}=\dfrac{1}{2}\sqrt{130-\dfrac{{{a}^{2}}}{2}}\sqrt{2a}-\dfrac{{{a}^{2}}}{2} \\
& 2{{a}^{2}}+\dfrac{{{a}^{2}}}{2}=\dfrac{1}{2}\sqrt{130-\dfrac{{{a}^{2}}}{2}}\sqrt{2a} \\
& \dfrac{5{{a}^{2}}}{2}=\dfrac{1}{2}\sqrt{130-\dfrac{{{a}^{2}}}{2}}\sqrt{2a} \\
\end{align}\]
On simplifying the above, equation we get;
\[\begin{align}
& \dfrac{5{{a}^{2}}}{\sqrt{2a}}=\sqrt{130-\dfrac{{{a}^{2}}}{2}} \\
& \dfrac{5a}{\sqrt{2}}=\sqrt{130-\dfrac{{{a}^{2}}}{2}} \\
\end{align}\]
Squaring both sides of the above equation, we get;
$\begin{align}
& \dfrac{25{{a}^{2}}}{2}=130-\dfrac{{{a}^{2}}}{2} \\
& \dfrac{250{{a}^{2}}}{2}+\dfrac{{{a}^{2}}}{2}=130 \\
& 13{{a}^{2}}=130 \\
& {{a}^{2}}=10..................\left( 10 \right) \\
\end{align}$
As area of the square is ${{a}^{2}}$ from equation (6) hence, area of square from equation (10) is 10.
Area of square is 10.
Hence option B is the correct answer.
Note: Another approach for this question would be that we can suppose $\angle AEB=\theta $ and as we know area of triangle ABC in terms of angle is given by;

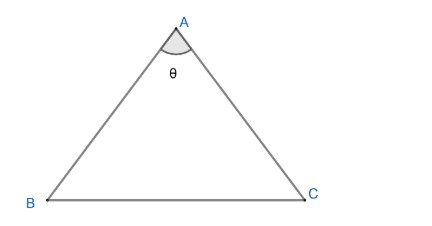
$=\dfrac{1}{2}AB.AC.\sin \theta $
So, area of triangle $EAB=\dfrac{1}{2}\times EA\times EB\sin \theta $
Where EA=EO-AO
$EB=\sqrt{130}$
ED can be calculated by $\Delta EOB$ and OA is $\dfrac{a\sqrt{2}}{2}$
$\sin \theta $ can be calculated by using triangle EOB where;
$\sin \theta =\dfrac{OB}{EB}$
$\text{Where }OB=\dfrac{a\sqrt{2}}{2}\And EB=\sqrt{130}$
And area of square$={{a}^{2}}$
Equate both the areas as given in question we will get${{a}^{2}}$.
Writing area of $\Delta EAB=\dfrac{Area\text{ }of\left( \Delta BED-\Delta ABD \right)}{2}$ is the key point of the solution.