Question

It is found that an equi-convex lens of radius of curvature $R$ is divided into two equal parts by a vertical plane. Therefore it becomes a Plano convex lens after the division. Suppose that the focal length of the equi-convex lens is given as $f$, then calculate the focal length of the Plano convex lens.

Answer 1

Hint: First of all draw the image of an equi-convex lens having a radius mentioned as per the question. An equi-convex lens is a lens with the two sides identical to each in the case of focal length, radius of curvature and all. This has to be kept in mind while solving the question.

Complete answer:
 First of all let us take a look at the image of an equi-convex lens.

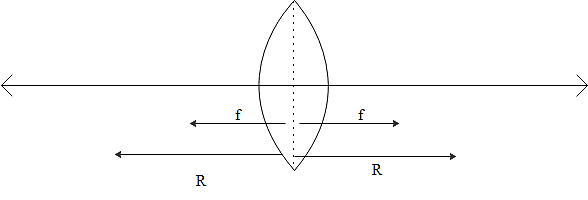
The image says that it is an equi-convex lens with a radius of curvature given as $R$. If we divide it symmetrically about its midpoint, then the equi-convex lens becomes two Plano convex lenses. As the both sides are identical in the equi-convex lens with radius of curvature as $R$ the focal length will be also the same for the two sides of the equi-convex lens. The focal length of a lens is can be expressed as the equation,
$f=\dfrac{1}{2}R$
When it is divided along the midpoint, the curved surface is not getting any kind of changes. Therefore their focal length will be the same as before. Therefore the answer for the question has arrived.

Note:
Plano-Convex lenses are useful mainly for the purpose of focusing the parallel rays of light to a single location. These kinds of lenses will be useful in order to focus, collect and collimate light. The asymmetry of such lenses will minimise the spherical aberration in some situations if the object and image are positioned at different distances from the lens.