Question

In the study of the Geiger-Marsden experiment on scattering of α-particles by a thin foil of gold, draw the trajectory of α-particles in the coulomb field of the target nucleus. Explain briefly how one gets the information on the size of the nucleus from this study:
From the relation$R={{R}_{0}}{{A}^{{}^{1}/{}_{3}}}$, where ${{R}_{0}}$ is constant and A is the mass number of the nucleus, show that the nuclear matter density is independent of A.

Answer 1

Hint: To show that nuclear matter density is independent of A, we need to find nuclear matter density. Nuclear matter density is the density of an atom’s nucleus. To find the density, we substitute the values of mass and volume of the nucleus in the equation for density.
Formula used:
Density,$\rho $ is given by
$\rho =\dfrac{M}{V}$

Complete step by step answer:
The trajectory of the α-particle in the coulomb field is given below.

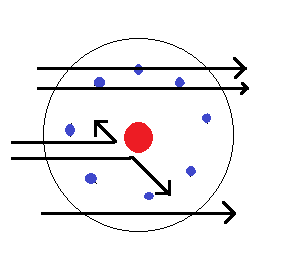
In the α-particles scattering experiment, most of the particles remained undeflected. Only a very small fraction of the particles deflected back. The α-particles are having positive charge and are deflected by the positive charge of the nucleus. So we can conclude that the nucleus occupies only a small volume of the total atom.
Let us assume that m is the mass of the nucleon and R is the radius of the nucleus. It is given that A is the mass number of the nucleus. So, the mass of the nucleus is given by,
$M=mA$
We assume that the nucleus is a sphere and the volume of the nucleus is given by,
$V=\dfrac{4}{3}\pi {{R}^{3}}$
It is given that $R={{R}_{0}}{{A}^{\dfrac{1}{3}}}$
$\Rightarrow V=\dfrac{4}{3}\pi {{\left( {{R}_{0}}{{A}^{\dfrac{1}{3}}} \right)}^{3}}$
On simplification, we get,
$V=\dfrac{4}{3}\pi {{R}_{0}}^{3}A$
Density of a material is defined as mass per unit volume. The density of the nucleus is given by,
$\rho =\dfrac{M}{V}$
Substituting the values of M and V, we get,
$\rho =\dfrac{mA}{\dfrac{4}{3}\pi {{R}_{0}}^{3}A}$
On simplification, we get,
$\rho =\dfrac{3m}{4\pi {{R}_{0}}^{3}}$
Thus nuclear matter density is independent of A.

Note:
The Geiger-Marsden experiment was done between the years 1908-1913 by Rutherford and his assistants Geiger and Marsden. This experiment gave the proof that JJ Thomson’s plum pudding model of atom and nuclei was a wrong conclusion.