Question

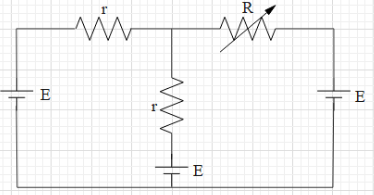
In the shown circuit the resistance $R$ can be varied. The variation of the current $i$ against $R$ is correctly plotted as:

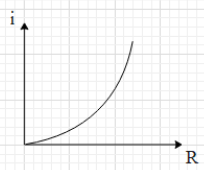
A.

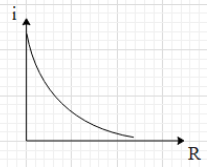
B.

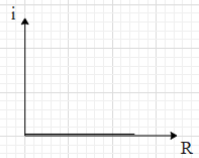
C.

D.

Answer 1

Hint: Assume any point to be at a potential of 0 volt and the point of junction of the three resistances to be at potential X. Then find the potential differences across each resistance and write the expressions for the currents by using Ohm’s law. Later, use junction law and find the expression for current in R.

Formula used:
$\Delta V=iR$

Complete step by step answer:
Let the potential in the lower section be 0 V, as shown in the figure. Let the potential at the junction of the three resistances (r, r, R) be X.Let the currents in the resistance r, r and R be ${{i}_{1}}$, ${{i}_{2}}$ and ${{i}_{3}}$, as shown in the figure.From the figure, we get that the potential differences across the resistance r, r and R are $E-X$, $E-X$ and $E-X$. Now, from Ohm’s law we get that $\Delta V=iR$, where $\Delta V$ is the potential difference across a resistance R and i is the current passing through R. Therefore, we can write that
$E-X={{i}_{1}}r$ ….. (i) (potential difference across resistance r).
$\Rightarrow E-X={{i}_{2}}r$ .… (ii) (potential difference across resistance r).
$\Rightarrow E-X={{i}_{3}}R$ (potential difference across resistance R).
From the equations (i) and (ii) we get that
${{i}_{1}}=\dfrac{E-X}{r}$ and ${{i}_{2}}=\dfrac{E-X}{r}$
From junction law, we get that ${{i}_{1}}={{i}_{2}}+{{i}_{3}}$ …. (ii).
Substitute the values of ${{i}_{1}}$ and ${{i}_{2}}$ in equation (ii).
$\Rightarrow \dfrac{E-X}{r}=\dfrac{E-X}{r}+{{i}_{3}}$
$\therefore {{i}_{3}}=0$.
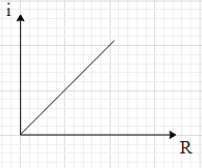
This means that the current in the resistance R is zero and it is independent of the value of R.Therefore, for every value of R, the current in it is zero.

Hence, the correct graph showing the variation of current in R with variation in R is shown in option C.

Note:Note that a positive charge always moves from a point at higher potential to a point at lower potential. Therefore, a current in a resistance is always directed from the end at higher potential to the other end that is at lower potential.