Question

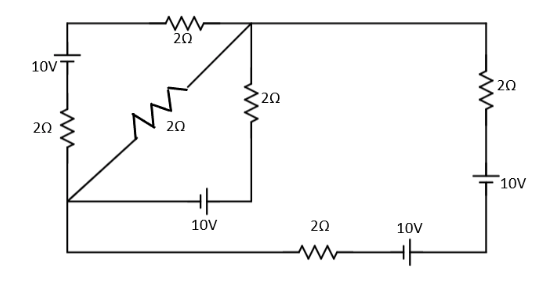
In the given circuit in Figure, all batteries have emf \[10V\] and internal resistance negligible. All resistors are in ohm. Calculate the current in the rightmost \[2\Omega \] resistor?

Answer 1

Hint-To solve the given problem consider the Junction rule and Loop rule. Usually these two rules or laws are very useful in finding the values of the electrical resistances of a complicated circuit.

Formula used:

$V = IR$

Where, $V$= voltage drop across the circuit, $I$= current flow across the circuit, $R$= resistance of the resistors.

Complete step-by-step solution:

By using the Kirchhoff’s current law,

In the left loop, both \[2\Omega \] resistors are in series combination so the total resistance on the left loop is,
$ \Rightarrow {\text{R = (2 + 2)}}$

By using the addition, we can add these two values, we get,

$ \Rightarrow {\text{4}}\Omega $

In the right loop, both \[2\Omega \] resistors are in series combination so the total resistance on the right loop is, ${\text{R = (2 + 2) = 4}}$
From Kirchhoff’s current law at ${X_X}$,

We get,

$\dfrac{{{\text{x - 10}}}}{4} + \dfrac{{{\text{x - 10}}}}{2} + \dfrac{{{\text{x - 20}}}}{4} + \dfrac{{{\text{x - 10}}}}{2} = 0$

Calculating we get the values of $X$ as:

$\therefore {\text{x = }}\dfrac{{35}}{3}V$

Therefore, the current flows through the circuit is,

 $ \Rightarrow {\text{I = }}\dfrac{{20 - \dfrac{{35}}{3}}}{4}$

We can use fraction division to solve the given equation. By making some simplifications we get,

$ \Rightarrow \dfrac{{25}}{{12}}A$

We can divide the given values to get the value of $I$. We get,

$\therefore 2.0833A$

Hence the current flows through the circuit is $2.0833A$

Additional information:
-An electric current is the flow of particles (electrons) through wires and components.
-It is the rate of flow of charge in the circuit.
-If the electric charge flows through a conductor, we can say that there is an electric current in the conductor.
-In the circuits using metallic wires, electrons constitute the flow of charges.

NoteTo solve the given problem first you need to remember the direction of flow of the current. The direction must be either clockwise or anti clockwise. Consider the current is flowing through a resistor, there will definitely be a potential decrease. In such a case the ohm’s law that is $V = IR$ will be negative.