Question

In the circuit shown, find the energy stored in \[1\mu F\] capacitor.

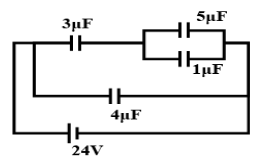
Answer 1

Hint: The ratio of the amount of electric charge deposited on a conductor to the difference in electric potential is known as capacitance. Self capacitance and reciprocal capacitance are two closely related concepts of capacitance. Self capacitance is a property of any material that can be electrically charged.

Complete step by step answer:
As capacitors are coupled in series, the overall capacitance is lower than the individual capacitances of the series capacitors. As two or more capacitors are connected in order, the result is a single (equivalent) capacitor with the cumulative total of the individual capacitors' plate spacings.
$\dfrac{1}{{{C_s}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
${C_p} = {C_1} + {C_2}$

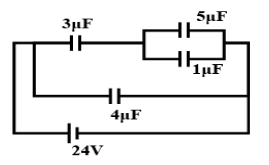
Here $5\mu F + 1\mu F = 6\mu F$(Since they are in parallel and Capacitance in parallel = ${C_p} = {C_1} + {C_2}$)
Hence the circuit becomes

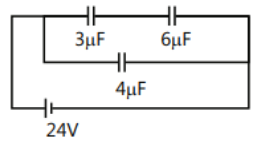
Here,
$\dfrac{1}{{{C_s}}} = \dfrac{1}{3}\mu F + \dfrac{1}{6}\mu F \\
\Rightarrow \dfrac{1}{{{C_s}}}= \dfrac{3}{6}\mu F \\
\Rightarrow \dfrac{1}{{{C_s}}}= \dfrac{1}{2}\mu F$
(Since they are in series and Capacitance in series = $\dfrac{1}{{{C_s}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$)
Hence, ${C_s} = 2\mu F$
Now $2\mu F\& 4\mu F$are in parallel.
Using ${C_p} = {C_1} + {C_2}$
${C_{net}} = 2 + {\text{ 4 = 6}}\mu {\text{F }}$
We know that
$q = CV$
Where $q$ = charge, $C$ = capacitance and $V$ = Volt.

So, substituting the values we get,
$Q = 6\mu F \times 24 = 144\mu C$
$144\mu C$ is getting divided between $2\mu F\& 4\mu F$. Hence,
$\dfrac{{{q_1}}}{4} = \dfrac{{{q_2}}}{2} \\
\Rightarrow {q_1} = 2{q_2}$
$ \Rightarrow {{\text{q}}_2} = \dfrac{{144\mu {\text{F}}}}{3} \\
\Rightarrow {{\text{q}}_2}= 48\mu {\text{C}}$
Here, $48\mu C$ is getting divided between $5\mu F\& 1\mu F$. Hence,
$\dfrac{{{q_3}}}{5} = \dfrac{{{q_4}}}{1} \\
\Rightarrow {q_3} = 5{q_4}$
The following is obtained
${{\text{q}}_6} = \dfrac{{48}}{6} \\
\Rightarrow {{\text{q}}_6}= 8\mu {\text{C}}$

The energy contained in a capacitor is the electric potential energy, which is proportional to the capacitor's voltage and charge. When a conductor's capacitance is C, it is initially uncharged and when attached to a battery, it acquires a potential difference V. If q is the current charge on the plate, then $U = \dfrac{1}{2}C{V^2}$
To calculate Energy the following formula is used
$U = \dfrac{1}{2}C{V^2}$
$\Rightarrow Q = 8\,C$
$\Rightarrow C = 1\mu F$
$\Rightarrow U = \dfrac{1}{2} \times 1 \times 8 \times 8 \\
\therefore U= 32\,\mu J$

Hence, the energy stored in \[1\mu F\] capacitor is $32\,\mu J$.

Note: The farad is the most common unit of capacitance measurement. One farad is equal to one second to the fourth power ampere squared per kg per square metre squared in SI units. A current flow of 1 A is generated when the voltage over a 1 F capacitor varies at a rate of one volt per second.