Question

In the circuit shown, a four-wire potentiometer is made of a 400cm long wire, which extends between A and B. The resistance per unit length of the potentiometer wire is $r=0.01 \Omega /cm$. If an ideal voltmeter is connected as shown with jockey J at 50 cm from end A, the expected reading of the voltmeter will be:-
A. 0.20V
B. 0.25V
C. 0.75V
D. 0.50V

Answer 1

Hint: Here potentiometer is acting as a simple source of resistance. Simple ohm’s law will produce an answer easily. If one is aware of the voltage divider formula, then too, one can solve such questions. A potentiometer is usually used as a source of variable resistor in a circuit.

Formula used:
The potential drop created across all the resistances is equal to the e.m.f. supplied (also a result of Kirchoff’s voltage law):
V=IR

Complete step by step answer:
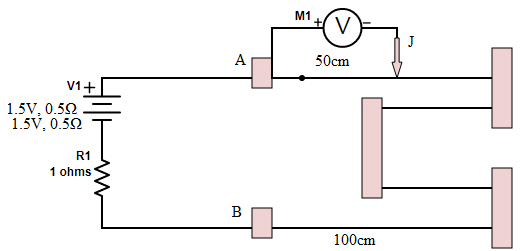
Our priority should be to find the total current flowing in the entire circuit. For that we will require total resistance and total potential difference value.
The potentiometer drawn in the circuit is merely providing us a resistance (let’s call it $R_2$) given by the product of its resistance per unit length and its total length:
$R_2 = 0.01 \Omega /cm \times 400cm = 4 \Omega $
Thus we get a resistance of $4 \Omega$ from the potentiometer.
Now, we have another resistance $R_1$ has given value 1$\Omega$.
The battery is a tricky one. It has two batteries labeled separately. Therefore, the internal resistance of the two batteries gives us a contribution of total 1$\Omega$.
Now, the total resistance in the circuit is obtained as:
$R_T = (4+1+1) \Omega = 6 \Omega$
The total current can now be obtained by dividing total voltage of (1.5+1.5)V by the above obtained total resistance.
Therefore,
$I_T = \dfrac{3V}{6 \Omega}$
$I_T = 0.5$A
Now, in the question is asked how much reading the voltmeter will show when the jockey is at 50cm length. A jockey is doing nothing here but just placing another end of the voltmeter for measurement. Thus, across the voltmeter there is a total resistance of:
$R = 0.01 \Omega /cm \times 50cm = 0.5 \Omega $
The potential drop across this can be simply found by multiplying the current with this resistance:
$V= 0.5 A \times 0.5 \Omega = 0.25V$

So, the correct answer is “Option A”.

Note:
Another way of doing this by using the voltage divider formula which is given as:
$V’ = \dfrac{R}{R_T} \times V$
Where V is the total emf (or potential difference) in the circuit and R is the resistance across which we need to find the potential drop and $R_T$ is the total resistance in the circuit.